

고급 위상 함수 처리와 볼륨에 대한 밉맵핑 기법 소개

- Rayleigh scattering : 작은 입자 → 빛을 고르게 산란
- Mie scattering (소/대 입자) : 입자가 클수록 전방향으로 강하게 산란됨 (Forward scattering)
→ 이 차이가 수식의 위상 함수 ρ(ω,ω′) 에 반영됨
오른쪽 아래 : 위상 함수 또는 산란 분포의 방향성을 시각화
- 원형 → 등방성 (Isotropic)
- 앞쪽 타원 → 전방 산란
- 뒤쪽 타원 → 후방 산란
ρ(ω,ω′)
- Phase Function은 광학 매질 내에서 빛이 어떤 방향으로 산란될지를 결정
- Rayleigh, Henyey-Greenstein, Schlick 등의 다양한 모델이 존재
- 볼륨 내부에서의 라이언스 전달을 설명하며, 위상함수 p는 산란의 방향성과 강도를 결정하는 핵심요소이다.
밉맵핑은 이러한 계산을 효율적으로 하기 위한 렌더링 최적화 기법으로 함께 소개될 예정

A Radiative Transfer Framework for Rendering Materials with Anisotropic Structure
(by Wenzel Jakob et al., Cornell University)
- 비등방성 미세 구조(microflakes)를 갖는 재질 (예: 섬유, 머리카락, 카펫) 렌더링 프레임워크
- 입사광이 재질의 방향성 구조에 따라 비대칭 산란되도록 모델링
- 전통적인 등방성(Isotropic) 모델보다 현실적인 표현 가능


The SGGX Microflake Distribution
(by Eric Heitz, Jonathan Dupuy, Cyril Crassin, Carsten Dachsbacher)
- SGGX (Spherical Gaussian-GGX) 모델은 미세 구조(마이크로플레이크)가 임의 방향으로 분포한 볼륨 기반 재질의 광산란을 정확하게 표현
- 미세한 입자의 방향 분포를 통해 헤어, 잎사귀, 구름 등의 렌더링 개선
- GGX 기반의 구조적 확장을 통해 볼륨 안에서의 조밀한 방향성 정보까지 반영 가능

“복잡한 현상을 표현하기 위해 볼륨(volume) 기반 모델을 사용하자”
→ 단순한 위상 함수(phase function)는 세부 묘사 능력이 떨어진다.
기존의 간단한 phase function은
- 입사광의 산란을 대칭적이고 단순하게 모델링
- 예: Isotropic scattering (등방성 산란)
- 결과적으로 디테일 부족, 현실감 낮음
"A Radiative Transfer Framework for Rendering Materials with Anisotropic Structure"
저자: Wenzel Jakob, Adam Arbree, Jonathan T. Moon, Kavita Bala, Steve Marschner (Cornell University)
- 복잡한 비등방성(anisotropic) 구조를 가진 재질을 위해
- 볼륨 내 마이크로 구조(micro-flakes)를 고려한 방사 전달 모델(radiative transfer framework)을 사용
- 비등방성 재질에 적합한 위상 함수 설계
- 섬유, 카펫, 헤어 등에서 현실적인 광 표현을 가능하게 함

- 기존 모델 (예: Henyey-Greenstein, Rayleigh 등) 은 특정 물리적 특성을 근사
- 그러나 복잡한 재질(예: 섬유, 안개, 피부 등)에서는 단순 위상 함수로 디테일이 손실됨
- 따라서 연구자들은 ρ를 보다 복잡하고 표현력 높은 함수로 바꾸고자 함

물리적 제약 조건 (Physical properties of ρ) : 임의의 함수를 넣을 수 있는 것처럼 보이지만, 다음 세 가지 물리적 조건을 만족해야만 실제 세계에 기반한 위상 함수가 된다.
- positivity (비음수성) : 위상함수는 음수일 수 없으며, 음의 산란량은 물리적으로 의미 없음
- reciprocity(상호성) : 광학적 역대칭성 보장. 빛이 𝜔′ → 𝜔 방향으로 산란되든, 𝜔 → 𝜔 ′ 방향으로 산란되든 확률은 동일
- energy conservation(에너지 보존) : 하나의 입사광이 여러 방향으로 퍼질수는 있어도, 총 에너지는 1(입사량 이상)을 넘을수 없다. 일부는 흡수되거나 전달되지 않음

- 기존에는 σₛ가 고정된 스칼라 값이었음 → 이제는 방향에 따른 함수 σₛ(ω) 로 바뀜
- 이는 매질이 방향에 따라 다르게 산란시키는 것을 반영함 (예: 나무 섬유, 머리카락, 패브릭)
Reciprocity (상호성)

→ 방향별 산란 계수를 고려한 상호성(산란 정도가 다르더라도 상호적 성질 유지해야 함)
- 기존 σₛ 모든 방향에 대해 일정한 산란 정도
- 개선된 σₛ(ω) 방향 ω에 따라 산란 정도가 달라짐
- 용도 섬유, 헤어, 브러시 등 방향성 구조가 있는 매질 표현에 필수
- 장점 더 정밀한 anisotropic volume rendering 구현 가능

Physical interpretation: non-spherical particles (microflakes)
→ 비구형 입자(편평한 형태의 마이크로 입자)의 산란 특성을 직관적으로 설명
- microflake 입자 : 얇고 납작한 형태 (flake = 조각)
- σₜ (Sigma_t) : Extinction Coefficient (소광 계수)
- σₜ는 광선이 입자와 충돌하거나 흡수될 확률을 의미.
- σₜ가 클수록 빛이 더 빨리 사라진다 (산란되거나 흡수되기 때문에).
- 입자 배열 방향 σₜ의 방향성에 결정적 영향
- 렌더링 영향 방향에 따라 빛의 감쇠가 달라짐 → Anisotropic Volume Rendering 구현 가능
좌측 그림: high σₜ
- 입자들이 수평 방향으로 놓여 있음
- 좌측에서 입사하는 광선은 많은 입자 표면과 충돌하게 됨
- 즉, 빛의 경로가 입자에 의해 자주 방해받음 → σₜ가 높음
우측 그림: low σₜ
- 입자들이 수직 방향으로 정렬되어 있음
- 위에서 수직으로 입사하는 광선은 입자 면을 거의 통과하게 됨
- 따라서 적은 충돌 → σₜ가 낮음

즉, 입자 분포로부터:
- 흡수 계수 (σₐ) : 특정 방향에서 얼마나 빛을 흡수하는지
- 산란 계수 (σₛ) : 얼마나 빛을 산란시키는지
- 위상 함수 (ρ) : 입사 방향 ω′에서 방향 ω로 얼마나 산란되는지
이 세 가지 물리량을 유도하는 것이 목표.

미세 입자(microflake)의 분포 및 속성을 이용해 다음의 방사 전파 특성을 계산한다:
- σₐ(ω) : 방향 ω에 대한 흡수 계수
- σₛ(ω) : 방향 ω에 대한 산란 계수
- ρ(ω, ω′) : 입사 방향 ω′에서 산란되어 방향 ω로 가는 위상 함수
입력 요소 (input)
- Particle density(입자밀도)
- 단위 부피당 microflake 입자의 수
- 방향에 따라 변하지 않음 (isotropic)
- albedo(알베도) α
- 입자가 반사하는 비율 (0~1 사이)
- 방향에 따라 변하지 않음
- 법선 분포 함수 (NDF) D(m)
- microflake의 법선이 방향 m에 분포하는 정도
- 마이크로페이스 이론과 유사한 개념
- 이 함수는 각 입자의 방향성 구조를 정의함
출력 요소 (output)
위 3가지 입력으로부터 다음을 도출:
- 흡수 계수 σa(ω)
- 산란 계수 σs(ω)
- 위상 함수 ρ(ω,ω′)
“Note: I present a less general version here for simplicity”
해당 설명은 단순화를 위해 방향성 변화를 고려하지 않는 모델로 제한하고 있음을 알립니다. 실제 일반화된 이론은 방향에 따라 변하는 σ, α 등을 포함합니다.
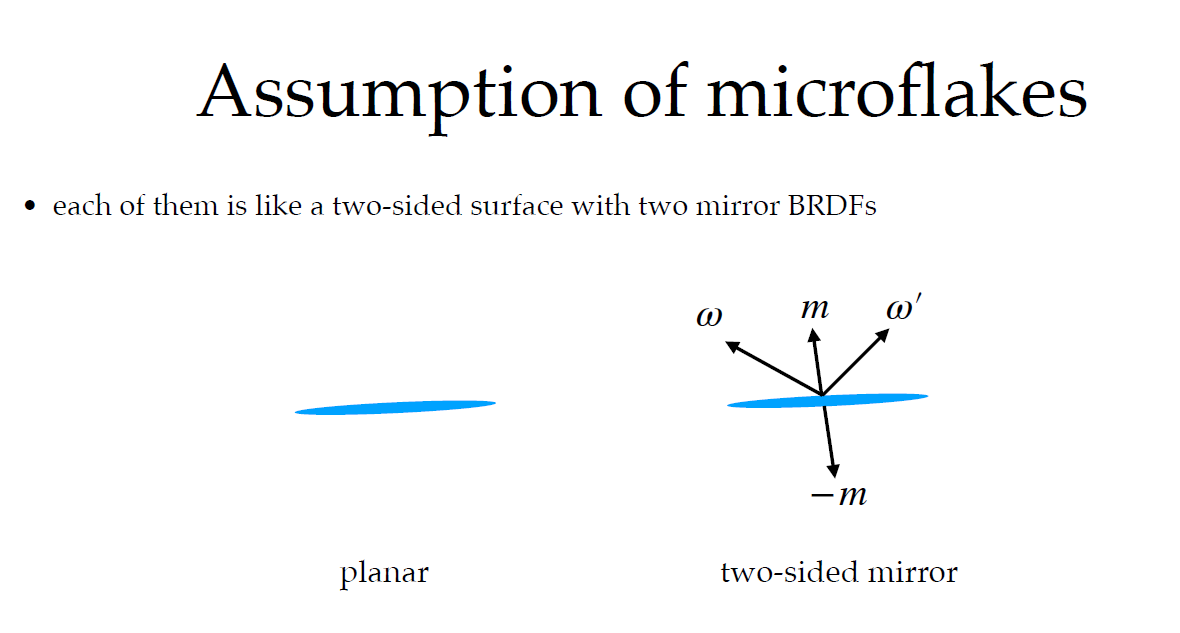
각 마이크로플레이크는 양면 거울 BRDF를 가진 평평한 이중면(two-sided surface)으로 간주된다.
planar
- 입자는 얇고 납작한 평면형 입자로 모델링됨.
- 3D 공간에서 정해진 법선 방향을 가진 "플레이크"로 존재.
two-sided mirror
- 입자는 거울처럼 빛을 반사하는 성질을 가짐.
- 방향 ω에서 입사된 광선은 플레이크의 법선 m을 기준으로 ω′ 방향으로 반사됨.
- 중요한 점: 양면 거울이므로, m과 -m 양쪽 모두 반사에 영향을 미침.
즉, 단일 면만 반응하는 것이 아니라, 두 방향 모두에서 입사된 빛이 반사될 수 있는 구조.
BRDF 관점에서
- 각 마이크로플레이크는 BRDF(양방향 반사 분포 함수)를 가짐.
- 이 BRDF는 mirror-like, 즉 반사만을 고려하는 델타 함수 기반.
- 산란의 방향성은 플레이크의 법선 분포 D(m) 에 따라 통계적으로 결정됨.

assuming the particles are planar(입자는 평면이라고 가정)

총 상호작용 계수 σt(ω)
빛이 입자와 만날 가능성:
- D(m) : 법선 분포 함수
- m⋅ω : 방향 ω에서의 입자의 투영면적 (교차 확률)
- 직관 : 광선이 입자 면에 수직으로 갈수록 만날 확률 ↑
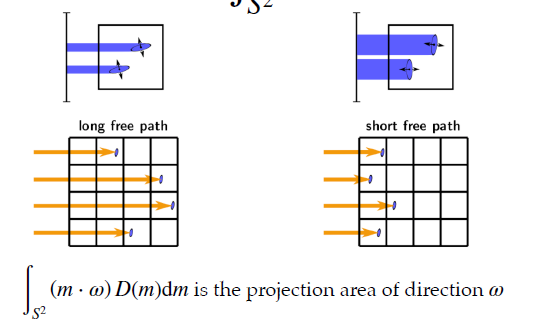
왼쪽 : 입사 방향이 입자 방향과 수평
→ 입자 면에 거의 수직하게 들어옴
→ 입자 투영 면적이 작음
→ 입자와의 교차 확률이 낮음
→ → 긴 free path (자유 평균 경로)
오른쪽: 입사 방향이 입자 방향과 수직
→ 입자 면에 수평하게 들어감
→ 입자 투영 면적이 큼
→ 입자와의 교차 확률이 큼
→ → 짧은 free path
즉, 입사 방향 ω에 따라 입자들과의 충돌 확률이 다르며, 이는 곧 free path에 영향을 준다는 걸 보여준다.

- 산란은 전체 충돌 중 α\alpha만큼
- 흡수는 나머지 (1−α)(1 - \alpha)
→ σt(ω)=σs(ω)+σa(ω) 성립

위상 함수 ρ(ω,ω′)
- 방향으로 입사한 빛이 ω′\omega' 방향으로 산란될 확률 밀도
- 핵심 아이디어 : 거울 반사 조건을 만족하는 법선 벡터 m 를 찾기 위한 조건 :

- 따라서, 이 방향을 갖는 마이크로플레이크(입자)가 있을 확률이 D(⋅)D(\cdot), 그리고 입사 반사 양면 모두 고려해야 하므로 두 개의 D 항이 곱해짐
- 마지막으로 정규화를 위해 σs(ω)로 나누어 줌 → reciprocity (상호성) 보장을 위해
상호성 보장 조건 (Reciprocity Condition)
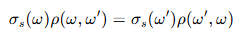
- 위상 함수는 입출 방향을 바꾸어도 물리적으로 같은 값을 가져야 함
- 이 수식을 만족하도록 ρ 정의가 설계됨
- 각 미세한 정사각형은 입자들이 분포한 지역 부피를 보여주며
- 파란 막대기(입자)에 빛이 입사된 뒤 ω′\omega' 방향으로 산란되는 것을 시각화
- 이 모든 확률은 D(m)D(m), ω\omega, ω′\omega'의 상호작용으로 결정됨

NDF는 마이크로플레이크 볼륨의 동작을 결정한다!
(a) NDF : D(ω) = cos^20(v, ω)+
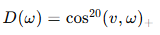
- 법선 분포가 vv 방향으로 매우 집중되어 있음
- → 입자들이 모두 수직 방향으로 정렬된 상태
- → 반사 특성이 거칠게 rough한 표면처럼 동작
→ ωi\omega_i 방향에서 들어온 빛이 NDF 중심 방향 vv에 대해 대칭 반사됨
오른쪽의 fp는 위상 함수(phase function)에 해당하는 분포.
(b) NDF: D(ω) = sin^20(v, ω)+

- 법선 분포가 vv 방향에서 수직 방향으로 퍼짐
- → 입자들이 vv를 **섬유 방향(tangent)**으로 가지며 평면에 눕는 형태
- → 이는 섬유(fiber) 또는 긴 기공을 가진 재료 같은 형태의 반사를 유도함→ 측면으로 넓게 산란됨
- NDF D(m)는 입자들의 배향 분포를 수학적으로 표현한 것으로,
- 그 분포가 달라지면, 결과적으로 빛이 마이크로플레이크 볼륨 내에서 어떻게 산란되는지 (즉, ρ(ω,ω′))도 완전히 달라짐
- 실제 재질(예: 머리카락, 흙먼지, 우유, 거친 금속 등)은 이 NDF에 따라 광학적 특성이 달라짐

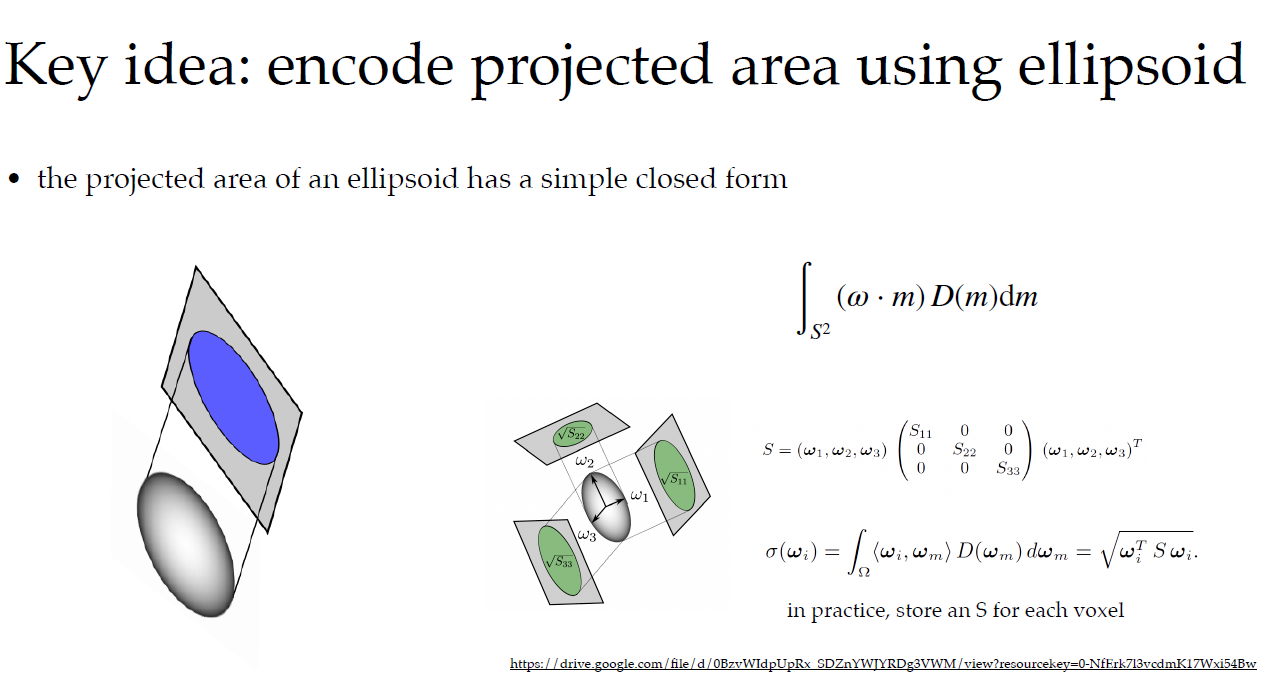
we want the projected area

to have closed-form
- 위 적분식(법선 분포를 따라 투영된 면적)이 닫힌 형태(closed-form), 즉 수학적으로 명확하게 계산 가능한 형태이기를 원한다.
- 이 적분은 산란/흡수 계수인 σs(ω), σa(ω) 등의 계산에 핵심적으로 사용되기 때문. 이게 해석적으로 간단하면 렌더링 성능이 향상.
we want D to be “filterable” like a normal map[LEAN, LEADR]
- 우리는 NDF가 필터링 가능하기를 원한다. 즉, 해상도를 낮추거나 mipmap을 만들 때 부드럽게 평균화할 수 있어야 한다.
- 참고 논문 : LEAN, LEADR은 NDF를 필터링 가능한 방식으로 사용하는 논문 이름.
- 보통 normal map을 사용해 디테일을 표현하는데, 이를 확대/축소해도 물리적으로 자연스러워야 하듯이, NDF도 비슷한 성질을 갖춰야 한다는 의미.

- 관련 위상 함수 예시
위상함수 상호성 에너지보존 특징 Isotropic ✅ ✅ 균일 산란 Rayleigh ✅ ✅ 미세 입자 산란 (파장 영향) Henyey-Greenstein ✅ ✅ 편향 산란 (anisotropy 표현) Schlick ✅ ✅ HG의 근사, 계산 단순함
'Technical Report > Graphics Tech Reports' 카테고리의 다른 글
| 2025 TA Campus 수업 문서 링크 (0) | 2026.01.20 |
|---|---|
| GPU Works Graphs(1) (0) | 2025.09.04 |
| GPU Specification compare PS5/XBOX Series X/Adreno/PC (0) | 2025.05.24 |
| [번역]Forward vs Deferred vs Forward+ Rendering with DirectX 11(2) Deferred Rendering (0) | 2025.05.12 |
| WGSL vs GLSL vs HLSL 문법 차이 (0) | 2025.05.01 |
