https://seb-v.github.io/optimization/update/2025/01/20/Fast-GPU-Matrix-multiplication.html
Introduction
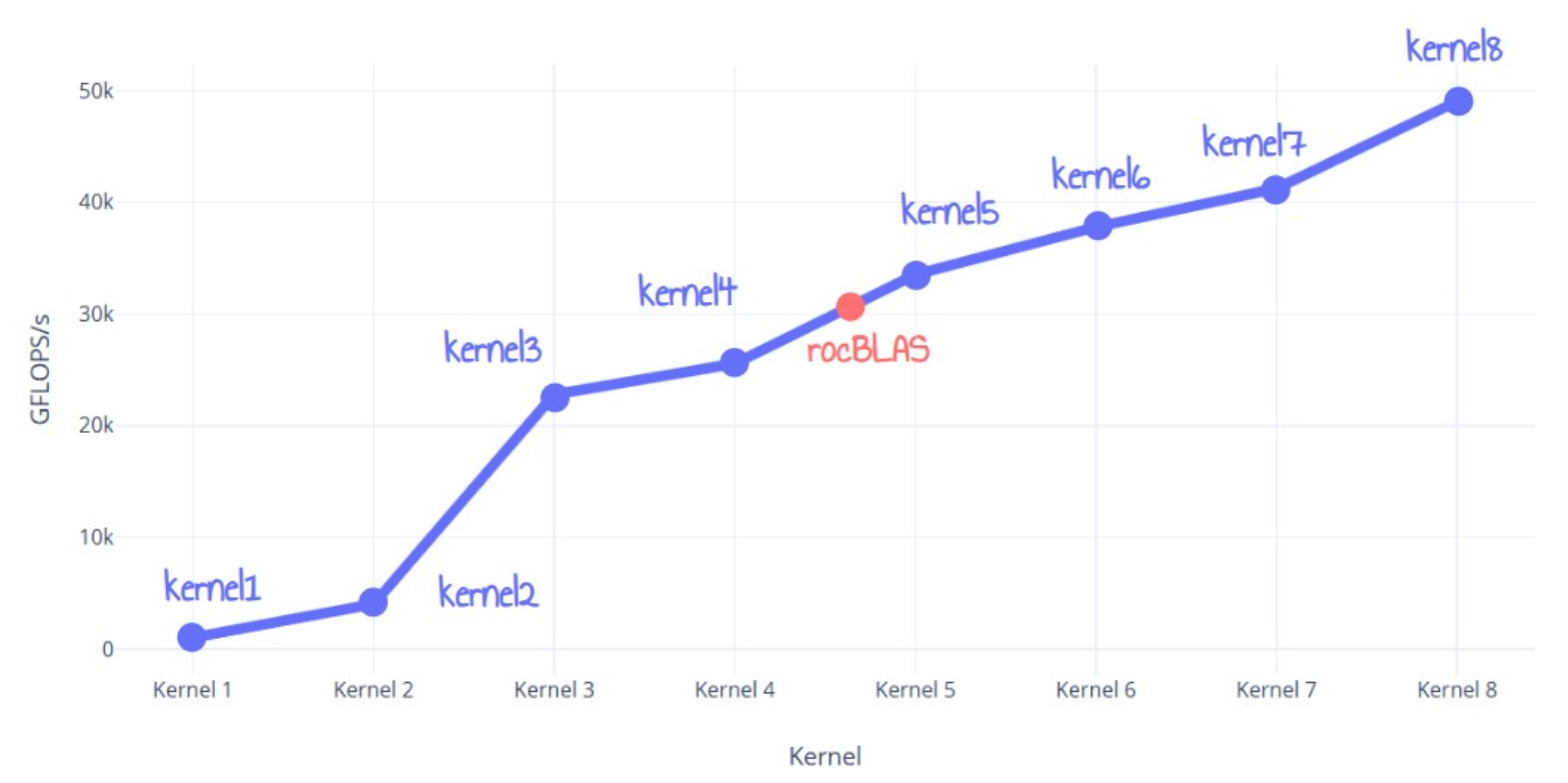
이 게시물에서는 AMD RDNA3 GPU에서 rocBLAS보다 60% 더 우수한 최적화된 FP32 행렬 곱셈을 작성하는 모든 단계를 공유하겠습니다. 몇 가지 기본 사항을 다루고 구현한 모든 최적화를 설명하겠습니다. 이는 8개의 다른 커널에서 반복적으로 수행됩니다.
저는 주로 RDNA3에 대한 이해를 심화하고 HIP 1을 시도해 보기 위해 이 작업을 하려고 했고, 이 작업을 하면서 배운 것을 공유해야 한다고 생각했습니다 :).
시작하기 전에 말씀드리고 싶은 몇 가지 사항 : 2
- 제가 사용한 모든 정보는 공개적으로 사용 가능한 ISA 가이드1에서 가져왔습니다.
- rocBLAS를 다시 구현하거나 교체할 생각은 없습니다.
- 단순성을 위해 4096x4096 행렬 단정밀도(FP32) 행렬 곱셈에만 집중했습니다.
- 모든 테스트는 AMD Radeon 7900 XTX가 있는 Windows 11에서 수행되었습니다.
자, 그럼 시작해보겠습니다.
Problem statement
요즘 행렬 곱셈의 성능을 개선하기 위한 많은 연구가 진행되고 있습니다. ML 애플리케이션의 핵심 알고리즘이기 때문에 활용할 수 있는 모든 FLOPS는 황금입니다.
진행하기 전에 행렬 곱셈의 기본 사항을 떠올려 보겠습니다. 두 행렬이 주어졌습니다.

곱 C는 다음과 같이 계산됩니다.
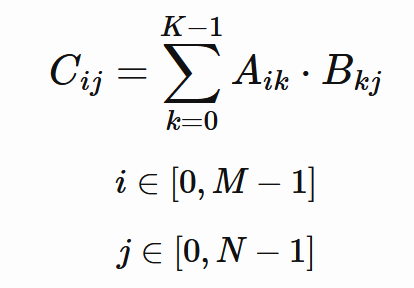
여기서 C는 크기 M, N의 결과 행렬입니다.
행렬 C의 각 출력 값에 대해 행렬 A의 행과 행렬 B의 열 간의 점곱을 계산합니다.
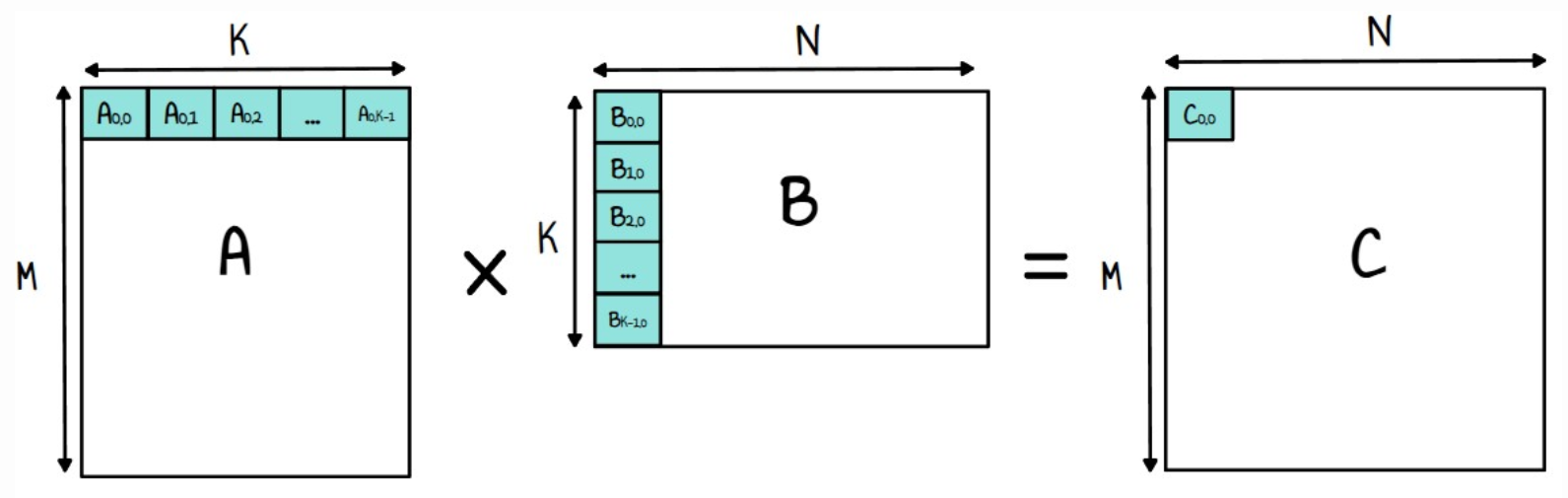
복잡성 측면에서 우리는 O(n^3)의 계산 복잡성과 O(n^2)의 메모리 접근을 가지고 있습니다. 아키텍처 세부 사항을 생각하지 않는다면, 이것은 분명히 컴퓨트 바운드 문제이며 우리의 목표는 GPU에서 Compute Bound3가 되는 것입니다.
7900 XTX에 가능한 최상의 구현을 작성했다고 가정해 보겠습니다. 얼마나 빨리 실행될 수 있을까요? 이 질문에 답하려면 RDNA3 아키텍처를 살펴봐야 합니다.
RDNA3 GPU는 WorkGroup Processor(WGP) 배열로 구성되어 있습니다. 모든 WGP는 2개의 Compute Unit(CU)으로 나뉘고, 그 자체도 2개의 SIMD로 나뉩니다. SIMD는 웨이브(CUDA의 경우 워프)로 구성된 여러 스레드의 작업을 처리하고 일부 작업(산술 연산 등)을 수행하는 구성 요소 집합을 갖습니다. 부동 소수점 연산의 경우 32방향 VALU 유닛이 2개 있습니다.
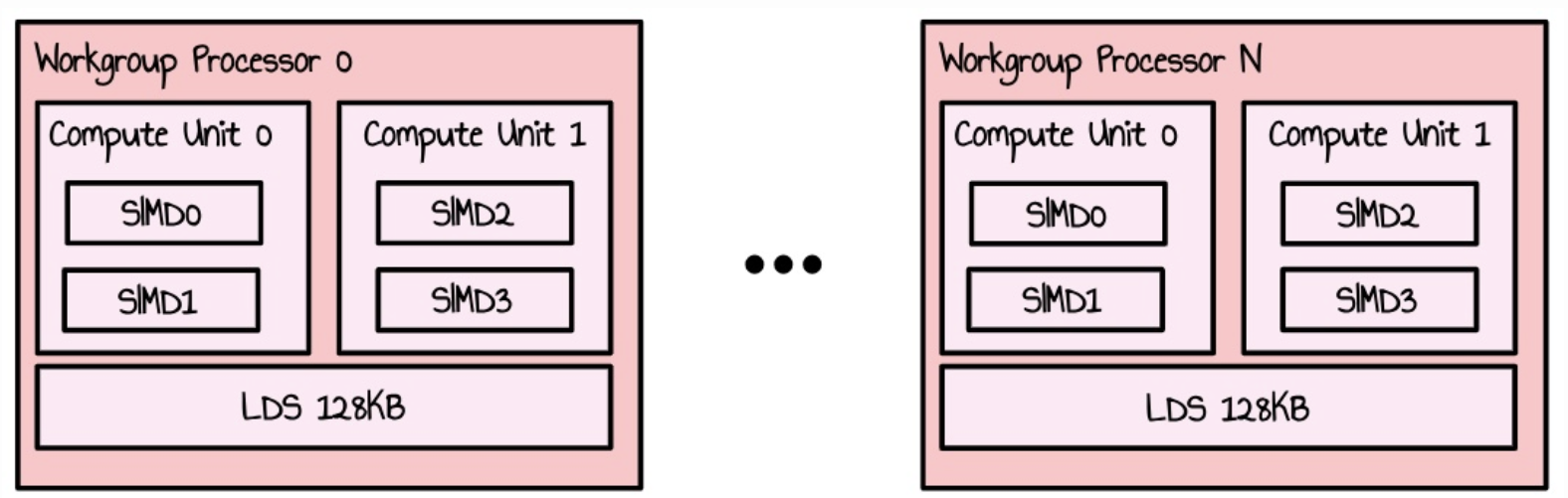
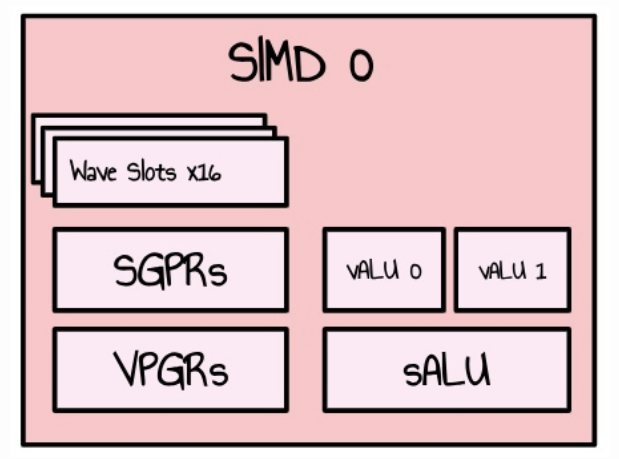
우리는 이 공식을 사용하여 초당 이론적인 부동 소수점 연산을 계산할 수 있습니다.
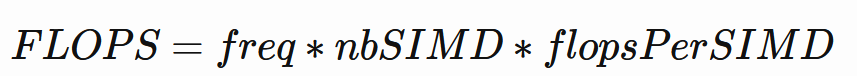
모든 SIMD는 사이클당 2개의 부동 소수점 명령어를 할당 수 있습니다(각 vALU 단위당 하나씩). FMA 명령어(Fused Multiply Add)를 사용하면 각 SIMD는 사이클당 32 * 2 * 2 = 128개의 부동 소수점 연산을 할당 수 있습니다. 7900 XTX에는 48개의 WGP가 있으며, 이는 48 * 2 * 2 = 192개의 SIMD입니다.
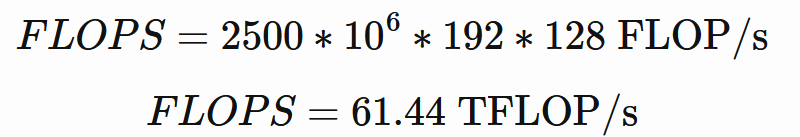
이론적인 VRAM 대역폭은 다음과 같습니다.

7900 XTX는 20Gbps로 작동하는 384비트 버스의 GDDR6를 사용합니다.
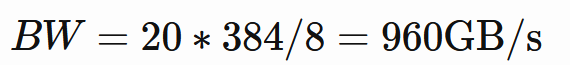
4096x4096 행렬 곱셈으로 다시 돌아가면 기본적으로 2 * 4096 * 4096 * 4096 연산을 수행해야 합니다. 61 TFLops 구현을 사용하면 작업을 수행하는 데 약 2.23ms가 걸리고 이 속도를 유지하는 데 필요한 대역폭은 다음과 같습니다.
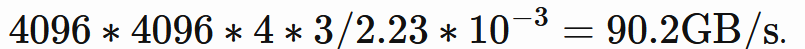
물론, 이는 메모리 계층 구조를 완전히 무시하기 때문에 너무 단순화된 계산이지만 사용 가능한 대역폭이 충분히 높기 때문에 읽는 데이터 양을 컴퓨팅 한계에 더 가깝게 늘릴 수 있습니다.
Kernel 1: naive implementation
다음과 같은 단순한 구현으로 시작해 보겠습니다.
__global__ void kernel1_naive(const float *A, const float *B, float *C, int M, int K, int N, float alpha, float beta) { int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; if (row < M && col < N) { float acc_c = 0.0f; for (int k = 0; k < K; ++k) { acc_c += A[row * K + k] * B[k * N + col]; } C[row * N + col] = alpha * acc_c + beta * C[row * N + col]; } } |
여기서 C = A * B 대신 C = alpha * A * B + beta * C를 한다는 것을 알 수 있을 것입니다. 이는 행렬 곱셈이 SGEMM 함수(단정밀도 일반 행렬 곱셈)에 의해 제공되는 rocBLAS와 같은 라이브러리와 비교하기 쉽기 때문입니다.
16x16의 블록 크기를 갖는 4096x4096 스레드를 시작하고 각 스레드는 이전에 설명한 내부 내적을 계산합니다.
이 커널의 성능은 136ms(1010.60 GFlops/s)입니다. 알다시피, 꽤 나쁘고 우리의 61 TFLops 목표와는 거리가 멉니다.
Kernel 0: rocBLAS reference implementation
이제 성능 측면에서 최악의 구현을 살펴보았으니 공식 rocBLAS 구현을 살펴보겠습니다.
const int M = N; const int K = N; CHECK_ROCBLAS_STATUS(rocblas_sgemm( handle, rocblas_operation_none, // Transpose option for A rocblas_operation_none, // Transpose option for B M, // Number of rows in A and C N, // Number of columns in B and C K, // Number of columns in A and rows in B &alpha, // alpha d_a, // Matrix A on the device M, // Leading dimension of A d_b, // Matrix B on the device K, // Leading dimension of B &beta, // beta d_c, // Matrix C on the device M // Leading dimension of C )); |
이전에 논의했듯이, 나는 alpha와 beta를 1.0으로 설정한 rocblas_sgemm 함수를 사용했습니다.4
이 커널의 성능은 4.49ms(30547 GFLOPs/s)입니다. 이는 분명히 우리의 커널 1보다 훨씬 뛰어나지만 여전히 우리의 이론적 61.4 TFlops/s와는 거리가 멉니다.
RGP5에서 ISA를 검사해보니 커널에서 듀얼 이슈 명령어를 찾을 수 없었습니다(v_fmac_f32_e32만 해당) 6
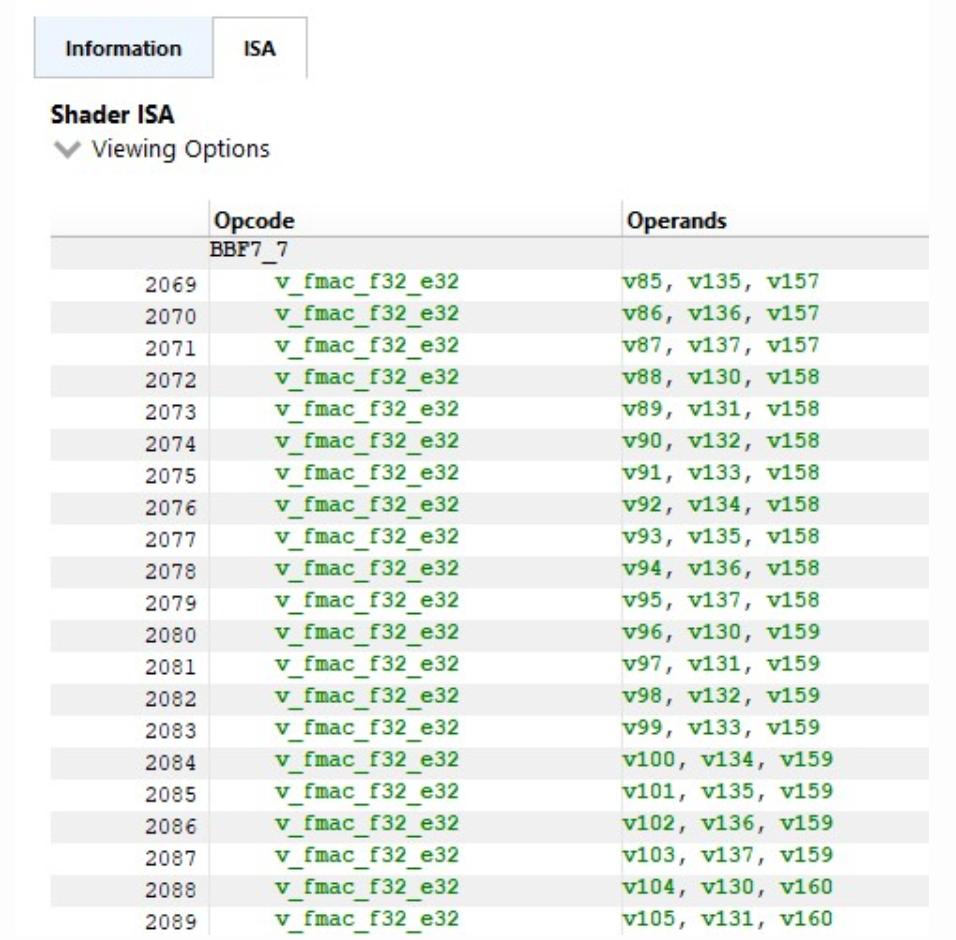
이는 본질적으로 VALU 유닛 중 하나가 아무것도 하지 않고 앉아 있다는 것을 의미하므로 매우 놀랍습니다.
이를 고려하면 이 커널의 VALU7 활용도는 매우 인상적이며 거의 100%입니다. 그러나 이러한 이중 이슈 명령을 제대로 활용할 수 없다는 것은 정말 놀랍습니다. 나중에 설명하겠습니다.
Kernel 2: LDS Tiling
우리의 단순한 커널의 주요 문제는 내부 루프가 글로벌 메모리에 직접 액세스한다는 것입니다. 글로벌 메모리에서 데이터를 가져오는 데는 일반적으로 수백 사이클 정도의 대기 시간이 걸리기 때문에 비효율적입니다. 각 메모리 읽기는 최소한의 계산(곱셈 한 번과 덧셈 한 번만)이 이어지기 때문에 GPU는 많은 수의 동시 스레드가 있어도 이 대기 시간을 숨기는 데 어려움을 겪습니다. 게다가 이 알고리즘은 여러 스레드에서 글로벌 메모리에서 동일한 행과 열을 반복적으로 읽어 중복 메모리 액세스가 발생하고 성능 병목 현상이 더욱 심화됩니다.
이 문제에 대한 해결책은 데이터를 더 빠른 로컬 메모리에 한 번 로드한 다음 모든 스레드에서 효율적으로 반복하는 것입니다. RDNA3에는 작업 그룹 내의 모든 스레드가 액세스할 수 있는 고속, 저지연 메모리인 로컬 데이터 저장소(LDS)가 있습니다.

LDS는 글로벌 메모리보다 용량이 훨씬 작기 때문에 타일링을 사용하여 문제를 더 작은 부분 행렬 곱셈으로 나누어야 합니다. 이를 용이하게 하는 한 가지 방법은 내부 루프의 내적을 외부 루프로 이동하여 계산을 재구성하는 것입니다. 핵심 아이디어는 행렬 A의 열과 행렬 B의 행을 캐시한 다음 전체 타일에서 계산을 수행하는 것입니다. 이 접근 방식은 캐시 효율성이 더 높고 메모리 액세스 대기 시간을 크게 줄입니다.
커널 1의 비슷한 코드는 다음과 같습니다.
for i from 0 to M - 1: # Loop over rows of A for j from 0 to N - 1: # Loop over columns of B sum = 0 for k from 0 to K - 1: # Loop over columns of A / rows of B sum += A[i][k] * B[k][j] end for C[ i ][ j ] = sum end for end for |
내적을 외부 루프로 이동하면 다음과 같습니다.
for k from 0 to K - 1: # Outer loop over the shared dimension for i from 0 to M - 1: # Loop over rows of A for j from 0 to N - 1: # Loop over columns of B C[i][j] += A[i][k] * B[k][j] end for end for end for |
이 양식의 타일링은 간단합니다. 각 작업 그룹은 타일에서 작동하고 다음 단계를 따릅니다. (배치 크기, 즉 LDS에 로드하는 행/열 수)
Init c to 0 While kId is less than N: # Load A and B to Tile As and Bs Load BK columns A to As Load BK rows to Bs Syncthreads # Accumulate results using LDS for k from 0 to BK c += As[threadIdx.y][k] * Bs[k][threadIdx.x] Syncthreads Increment kId by BK end for c[row][col]=c |
타일 크기를 32x32로 선택하고 BK = 32이면 새로운 커널은 다음과 같습니다.
#define TILE_SIZE 32 __global__ void kernel2_lds(const float *A, const float *B, float *C, int N) { __shared__ float As[TILE_SIZE][TILE_SIZE]; __shared__ float Bs[TILE_SIZE][TILE_SIZE]; int row = blockIdx.y * TILE_SIZE + threadIdx.y; int col = blockIdx.x * TILE_SIZE + threadIdx.x; float sum = 0.0f; for (int t = 0; t < N; t += TILE_SIZE) { Bs[threadIdx.y][threadIdx.x] = B[N * (threadIdx.y + t) + col]; As[threadIdx.y][threadIdx.x] = A[N * row + t + threadIdx.x]; __syncthreads(); for (int k = 0; k < TILE_SIZE; k++) { sum += As[threadIdx.y][k] * Bs[k][threadIdx.x]; } __syncthreads(); } if (row < N && col < N) { C[row * N + col] = sum; } } |
__syncthreads();는 작업 그룹의 모든 스레드가 LDS에 로드된 데이터를 보고 데이터에 대한 업데이트가 이루어지기 전에 동기화할 수 있도록 하는 데 필요합니다.
또한 행렬 A와 B의 내용이 열이 아닌 행으로 LDS에 로드되어 병합되지 않은 메모리 액세스가 발생하지 않도록 합니다. 실제로 열로 읽으려면 웨이브의 각 스레드가 비연속 메모리 영역에 액세스하여 여러 개의 별도 트랜잭션이 발생하고 아래 2개의 다이어그램에 표시된 것처럼 효율성이 감소합니다.


ISA 가이드에 따르면, 장치 메모리는 32, 64 또는 128바이트 트랜잭션을 통해 액세스되며, 이는 자연스럽게 정렬되어야 합니다. 메모리 처리량을 극대화하려면 웨이브 내의 스레드 간에 메모리 액세스를 통합하여 트랜잭션 수를 최소화해야 합니다8
이 커널의 성능은 34.2ms(4017 GFlops/s)입니다. 이는 우리의 단순한 커널보다 4배 빠릅니다!
| Kernel # | Description | Time(ms) | Performance(GFLOPS) | Relative Performance to rocBLAS (rocBLAS에 대한 상대적 성능) |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
RGP를 사용하여 무슨 일이 일어나고 있는지 이해해 보겠습니다. 우리의 점유율은 꽤 좋지만(100%) VALU 활용도는 15%에 불과합니다.
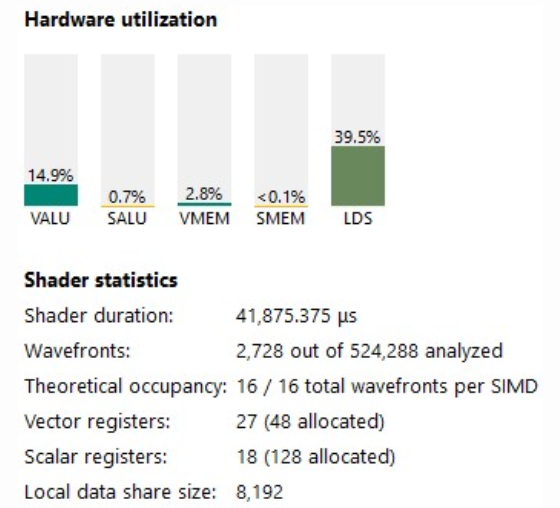
명령어 타이밍 탭에서 ISA를 살펴보면 몇 가지 흥미로운 점이 보입니다.
- 내부 루프가 펼쳐졌습니다.
- v_dual_fmac_f32를 사용하지 않고 rocBLAS처럼 v_fmac_f32만 사용합니다.
- 이러한 LDS 로드에서 일관된 90사이클 정지(숨겨지지 않음)가 발생합니다(s_waitcnt lgkmcnt(X) 명령어 확인)
Unrolling 9

무슨 일이 일어나고 있는지 이해하려면 SIMD 스케줄링이 어떻게 작동하는지 빠르게 설명해야 합니다. 각 클록 사이클 동안 SIMD는 웨이브 풀에서 명령을 선택하여 실행합니다. SIMD는 최대 16개의 웨이브프런트 10를 병렬로 관리할 수 있습니다. 점유에 대해 언급할 때 실제로는 SIMD가 지원할 수 있는 이론적 최대 웨이브 수에 대한 활성 웨이브의 비율에 대해 이야기하고 있습니다. 활성 웨이브프런트가 많을수록 SIMD가 웨이브 간에 전환할 가능성이 커지고 개별 웨이브프런트 내에서 지연 시간을 숨길 가능성이 높아집니다.
우리의 사례로 돌아가면, 우리는 아마도 다음과 같은 것을 갖게 될 것입니다.
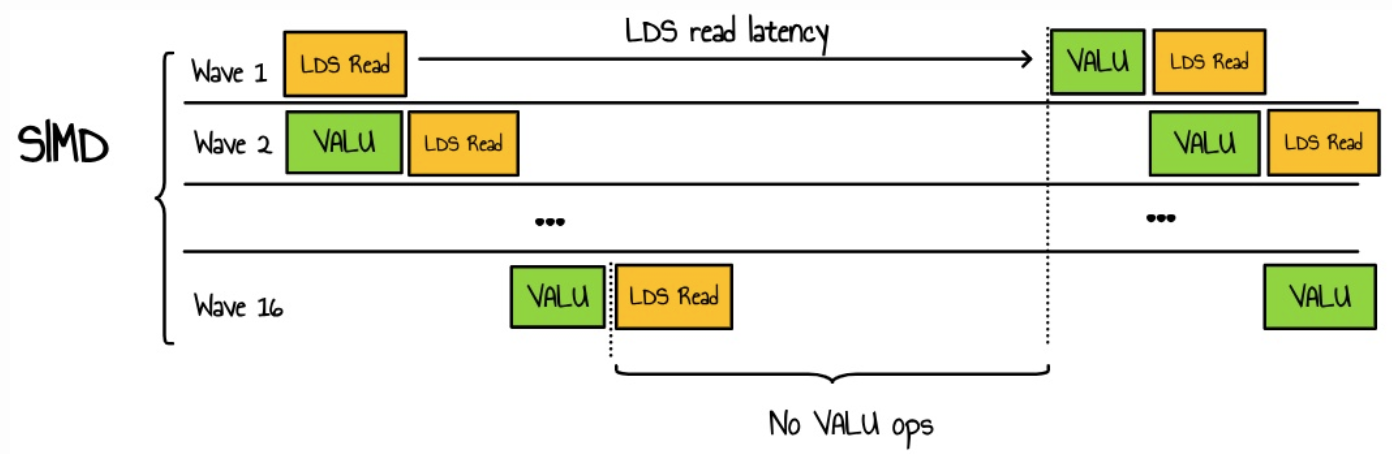
여기서 우리는 병렬로 많은 웨이브를 시작하는 고점유 커널을 가지고 있으며, 모두 LDS에 대한 액세스를 위해 경쟁합니다. VALU 연산에 걸리는 시간이 LDS 대기 시간보다 짧기 때문에 추가 스레드가 있어도 대기 시간을 숨길 수 없습니다. 이는 대기 시간으로 인해 LDS 대역폭 혼잡과 리소스 낭비를 초래합니다.
이 문제를 해결하는 한 가지 방법은 커널의 산술 강도를 높여 웨이브당 VALU 연산이 LDS 메모리 읽기보다 오래 걸리도록 하는 것입니다.
Kernel 3 : Register tiling
이제 커널의 산술적 복잡도를 높이고자 합니다. 즉, 각 스레드가 더 많은 계산을 수행하도록 하는 것입니다. 기본적으로, 우리는 계산 대 데이터 읽기 비율을 높이는 것을 목표로 합니다. 이를 달성하는 한 가지 방법은 스레드당 작은 출력 타일(예: 8x8 타일)을 계산하는 것입니다. 이를 위해 추가 타일링 수준을 도입합니다.
각 스레드는 출력 행렬의 작은 타일을 생성하는 역할을 합니다. 행렬 A와 B의 내용을 레지스터에 캐시하여 매우 낮은 지연 시간 액세스를 가능하게 할 수 있습니다. 그러나 레지스터는 GPU에서 제한되어 SIMD당 1536개의 VGPR(벡터 범용 레지스터)과 커널당 최대 256개의 레지스터를 사용할 수 있습니다. 레지스터 사용량이 증가하면 SIMD당 많은 웨이브를 시작할 수 없으므로 점유율이 효과적으로 감소합니다. 그러나 몇 개의 웨이브만으로 SIMD의 VALU(벡터 산술 논리 단위) 활용을 극대화할 수 있다면 이는 문제가 되지 않을 것입니다.
이제 타일링의 다양한 수준을 살펴보겠습니다.
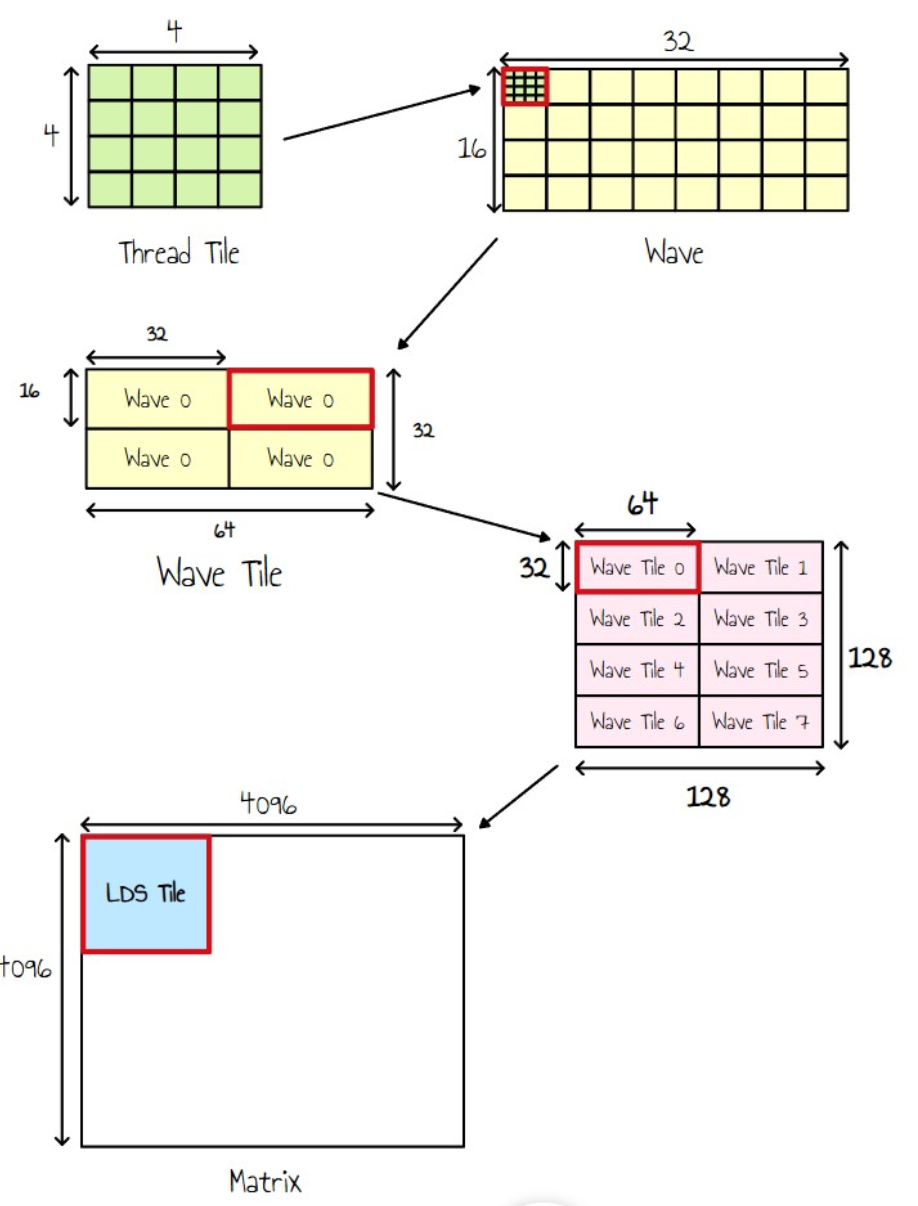
- 각 스레드는 이제 4x4 블록(스레드 타일)을 출력합니다.
- 웨이브는 32개의 스레드로 구성되므로 이를 8x4 블록으로 구성하여 단일 웨이브가 32x16 타일을 출력하도록 합니다.
- 작업 그룹당 256개의 스레드(즉, 웨이브 8개)가 있으므로 이를 웨이브 타일의 2x4 그리드로 구성합니다.
- 각 웨이브는 2x2 그리드를 반복하여 전체 웨이브 타일을 덮습니다.
기본적으로 이는 각 스레드가 이제 8x8 출력 타일을 계산할 책임이 있음을 의미합니다.
커널 매개변수는 다음과 같습니다.
#define BLOCK_SIZE 256 // Block Tile size constexpr int BN = 128; constexpr int BM = 128; // Number of Row or column we read per batch constexpr int BK = 8; // Thread Tile size . 4x4 constexpr int TN = 4; constexpr int TM = 4; // A wave is a block of 8x4 of the output matrix constexpr int nbThreadXPerWave = 8; constexpr int nbThreadYPerWave = 4; // Number of waves in a block constexpr int nbWavesPerBlock = BLOCK_SIZE / 32; constexpr int WN = 64; constexpr int WM = BN * BM / nbWavesPerBlock / WN; constexpr int nbIterWaveN = WN / (nbThreadXPerWave * TN); constexpr int nbIterWaveM = WM / (nbThreadYPerWave * TM); // LDS Tile __shared__ float As[BK][BM]; __shared__ float Bs[BK][BN]; // Column and row from A and B, stored into registers float A_col[nbIterWaveM * TM]; float B_row[nbIterWaveN * TN]; //Wave Tile (registers) float C_regs[TM * nbIterWaveM * TN * nbIterWaveN] = {0.0f}; |
새로운 커널에 대한 비슷한 코드:
Initialize kId to 0 While kId is less than N: # Loading Tile to LDS Load BK columns from A to As Load BK rows from B to Bs Syncthreads For k from 0 to BK - 1 do: Load col k of As to A_col Load row k of Bs to B_row # Wave Tile For idY from 0 to nbIterWaveM: For idX from 0 to nbIterWaveN: # Thread Tile For i from 0 to TM: For j from 0 to TN: x = idX * TN + j; y = idY * TM + i; C_regs[y][x] = A_col[y] * B_row[x] Syncthreads Increment kId by BK Write C_regs to C |
전체 커널 소스 코드는 여기에서 찾을 수 있습니다.
이 커널의 성능은 6.03ms(22777 GFlops/s)로 이전 커널보다 5배 빠릅니다!
| Kernel # | Description | Time(ms) | Performance(GFLOPS) | Relative Performance to rocBLAS (rocBLAS에 대한 상대적 성능) |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
점유율은 낮지만 VALU 활용도가 크게 증가했습니다.
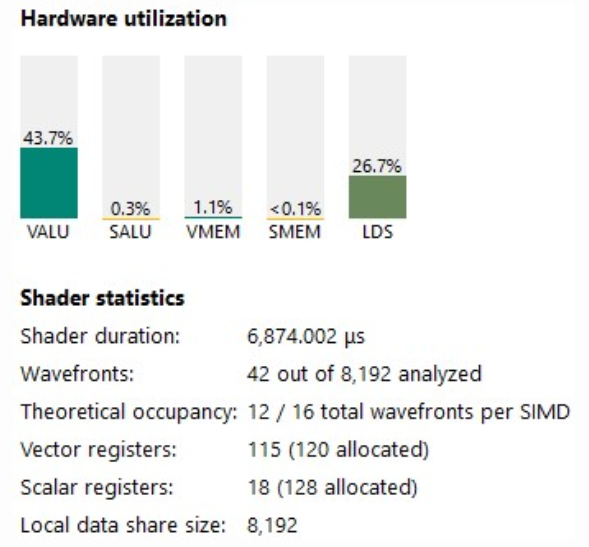
ISA가 좋아 보입니다. 이제 우리는 많은 v_dual_fmac 명령어를 가지고 있습니다. 일부는 여전히 단일 fma이지만, 정확히 우리가 원했던 것입니다.

이것이 Kernel 2에 비해 상당히 개선되었지만, 우리는 여전히 LDS를 기다리고 있다는 것을 알 수 있습니다. 이는 특히 첫 번째 ds_load 명령어 배치에서 그렇습니다. 아래에서 볼 수 있듯이 누적 비숨김 대기 시간이 100개 이상인 것을 관찰합니다.

이것에 뛰어들기 전에, 먼저 글로벌 메모리에서 읽는 방식을 개선해야 합니다. RGP에 따르면, 이것이 현재 성능 측면에서 가장 큰 병목 현상입니다.

글로벌 메모리 대기에 대한 누적 대기 시간은 1,200만 클럭 사이클을 초과하는데, 이는 내부 루프의 LDS 로드 대기 시간보다 4배 더 큽니다.
성능을 더욱 최적화하기 위해 글로벌 메모리 읽기 대기 시간을 더 잘 숨기는 데 집중할 것입니다.
Kernel 4 : GMEM double buffering
현재 구현에서는 모든 웨이브가 작업을 수행하기 전에 전역 메모리를 기다린 후 LDS 쓰기 대기 시간을 기다려야 합니다. 점유율이 높은 시나리오에서는 GPU가 이 대기 시간을 숨길 다른 웨이브를 찾을 수 있다면 문제가 되지 않습니다. 그러나 실제로는 전역 메모리에서 읽기 전후에 동기화 스레드를 사용하기 때문에 동일한 상태의 여러 웨이브가 동시에 실행되는 경우가 많습니다.

이를 완화하는 한 가지 방법은 이중 버퍼링을 사용하는 것입니다. 메모리를 두 배로 할당하고 LDS에 대한 읽기 및 쓰기를 병렬로 수행할 수 있습니다.
또는 중간 레지스터를 사용하여 LDS에서 작업하는 동안 글로벌 메모리에서 데이터를 로드하고 필요하기 직전에만 LDS에 쓸 수 있습니다. 이렇게 하면 글로벌 메모리에서 기다리지 않아도 됩니다.
나는 아직 내부 루프에 추가 LDS 압력을 도입하고 싶지 않기 때문에 지금은 이 접근 방식을 선호합니다.
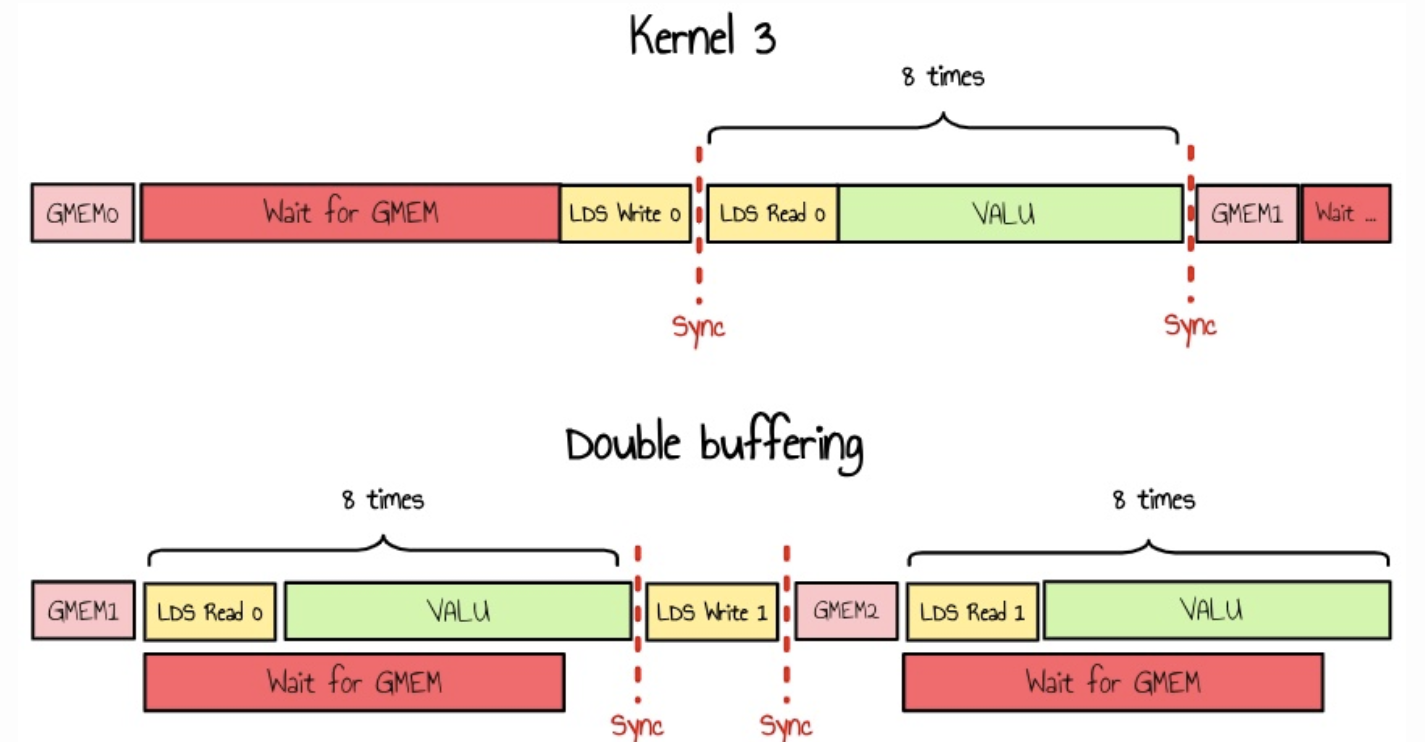
의사 코드를 업데이트하면 다음과 같은 결과가 나타납니다.
Initialize kId to 0 # Load first batch before loop Load BK columns from A to As Load BK rows from B to Bs Syncthreads While kId is less than N: # Loading Tile to LDS Load BK columns from A to A_TMP (no wait) Load BK rows from B to B_TMP (no wait) For k from 0 to BK - 1 do: Load col k of As to A_col Load row k of Bs to B_row # Wave Tile For idY from 0 to nbIterWaveM: For idX from 0 to nbIterWaveN: # Thread Tile For i from 0 to TM: For j from 0 to TN: x = idX * TN + j; y = idY * TM + i; C_regs[y][x] = A_col[y] * B_row[x] Syncthreads Save A_TMP and B_TMP to As and Bs Syncthreads Increment kId by BK Write C_regs to C |
놀랍게도 이 커널의 성능은 14.3032ms(9612.48 GFLOPS)로 감소했는데, 이는 커널 3보다 2배 이상 느립니다!
저희의 더블 버퍼링 알고리즘은 더 많은 레지스터를 활용하고 점유율을 줄입니다. RGP에서 ISA를 검사한 후, HIP 컴파일러가 스크래치 메모리를 대신 사용하여 레지스터 사용량을 낮추려고 시도하는 것을 알 수 있습니다. 이는 성능에 해롭습니다.

안타깝게도 HIP에서 커널당 최대 레지스터 수를 직접 설정할 수 없습니다(이론적으로는 256개). 그러나 launch_bounds 확장을 사용하여 컴파일러에 힌트를 제공할 수 있습니다.
이 변경으로 성능이 정상으로 돌아왔습니다: 5.37ms(25559.6 GFLOP/s).
전체 커널 소스 코드는 여기에서 찾을 수 있습니다.
| Kernel # | Description | Time(ms) | Performance (GFLOPS) |
Relative Performance to rocBLAS |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
| Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7% |
VALU 활용률이 43%에서 52%로 증가했습니다.
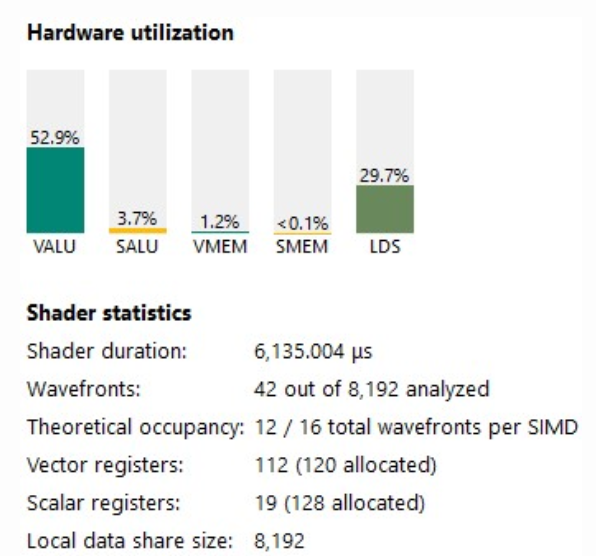
아래에서 볼 수 있듯이, 새로운 병목 현상이 된 내부 루프의 LDS 로드로 돌아갈 수 있습니다.

Kernel 5 : Optimize LDS usage
이전 커널에서 살펴보지 않은 한 가지는 LDS에서 뱅크 충돌이 있었는지 여부입니다. 이 정보는 실제로 RGP에서 쉽게 접근할 수 없습니다. LDS에 쓰는 ISA 섹션을 살펴보면 대기 시간이 예상치 못하게 높다는 것을 알 수 있습니다.

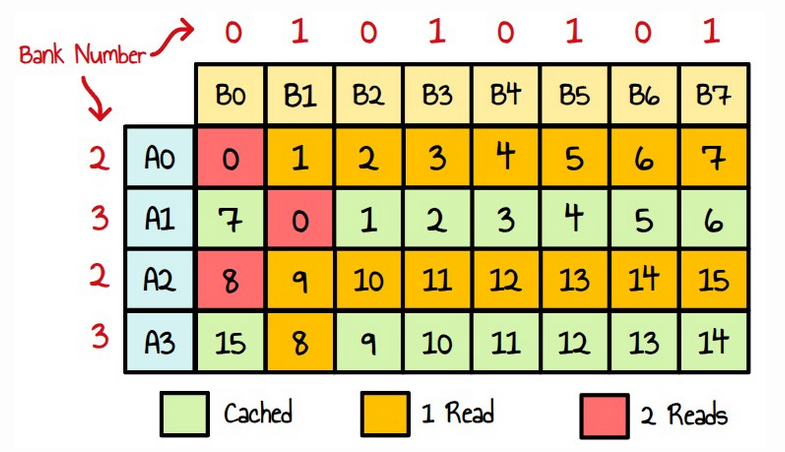
RDNA3 프로그래밍 가이드에 따르면 LDS 메모리는 64개의 DWORD-wide RAM 뱅크로 분할됩니다. 이 64개의 뱅크는 각각 32개의 뱅크로 세분되며, 각 뱅크 중 32개는 SIMD32 한 쌍과 제휴하고, 다른 32개의 뱅크는 WGP 내의 다른 SIMD32 한 쌍과 제휴합니다. 각 뱅크는 512x32 2포트 RAM(클럭 사이클당 1R/1W)입니다. DWORD는 뱅크에 직렬로 배치되지만 모든 뱅크는 동시에 저장 또는 로드를 실행할 수 있습니다.
따라서 웨이브 내의 스레드가 같은 뱅크에 액세스하는 경우 메모리 트랜잭션이 직렬화되는데, 이는 행렬 A의 열을 A에 쓸 때 발생하는 일과 정확히 같습니다.

현재 커널은 행렬 A의 내용을 행별로 읽어서 병합되지 않은 메모리 로드를 방지합니다. 그런 다음 행렬 A의 열에서 연산을 수행하면 행렬 A를 행렬 As로 전치하여 As의 각 줄이 A의 타일 열에 해당하도록 합니다.
이제 이 작업이 웨이브에 어떻게 매핑되는지 살펴보면 각 웨이브 내에서 4개의 연속된 뱅크에 기본적으로 8번 쓴다는 것을 알 수 있습니다. 이를 수정하는 한 가지 방법은 LDS 행렬 As에 4개의 요소 패딩을 추가하는 것입니다.
__shared__ float As[BK][BM+4]; // 4 padding to avoid bank conflicts |
이 변경 사항으로 다른 RGP 캡처를 수행합니다.

LDS 대기 시간이 크게 감소했고 VALU 사용률은 이제 62.3%입니다.
그러나 커널은 여전히 이러한 LDS 부하에 의해 제한됩니다. 냅킨 수학 11을 수행하고 LDS 대역폭의 한계에 도달하지 않았는지 확인해 보겠습니다.
앞서 말했듯이 각 SIMD 쌍에는 DWORD를 읽을 수 있는 32개 뱅크 메모리가 있습니다. 이론적 대역폭은 다음과 같아야 합니다.
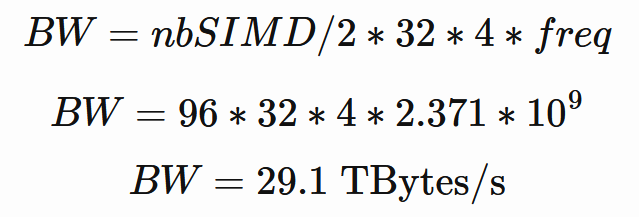
이제 현재 알고리즘이 무엇을 하는지 분석해 보겠습니다.
- 각 스레드는 반복당 행렬당 8개의 DWORD를 읽습니다(8x8의 동등 스레드 타일)
- 웨이브는 총 32x8x2개의 DWORD를 읽습니다.
- 작업 그룹에는 웨이브가 8개 있으므로 반복당 4096개의 읽기가 있습니다. 반복이 4096개이므로 작업 그룹당 4096x4096x4바이트를 읽습니다.
- 작업 그룹이 32x32이면 총 68719476736바이트입니다.
읽기용입니다. LDS에도 씁니다 : 4096x128x32x32x4x2 = 4294967296바이트.
현재 실행 시간이 5.37ms이므로 필요한 LDS 대역폭은 약 13.56TBytes/s입니다. 이는 최대 용량의 46%보다 작지만 여러 웨이브가 동시에 읽거나 쓰려고 할 때 커널이 LDS에서 혼잡을 경험할 가능성이 높습니다.
이를 완화하기 위해 다음 두 가지를 시도할 수 있습니다.
- CU 모드 활성화
- LDS 읽기와 GMEM 읽기를 교환하기 위해 산술 강도를 다시 높입니다.
RDNA3 프로그래밍 가이드에 따르면 LDS는 WGP 모드와 CU 모드의 두 가지 고유한 모드에서 작동할 수 있습니다. HIP는 기본적으로 WGP 모드를 사용합니다. WGP 모드에서 LDS는 WGP의 모든 파동이 액세스할 수 있는 하나의 큰 연속 메모리이므로 LDS에서 혼잡이 발생할 가능성이 더 큽니다. CU 모드에서 LDS는 각각 두 개의 SIMD32를 제공하는 별도의 상위 및 하위 LDS로 효과적으로 분할됩니다. 파동은 파동이 실행되는 SIMD와 연관된 LDS의 절반 내에서 LDS 공간이 할당됩니다. CU 모드를 활성화하면 LDS8에 대한 파동 경합 가능성을 줄여야 합니다.
시도할 수 있는 두 번째 방법은 스레드 타일을 8x8 대신 16x8로 늘리는 것입니다. 이렇게 하면 계산 대 데이터 읽기 비율이 향상됩니다. 여전히 커널에 대한 256 VGPR 예산 내에 들어맞아야 하며 대역폭 요구 사항을 10.3 TBytes/s로 줄여야 합니다.
이 모든 변경 사항을 적용하면 이 커널의 성능은 이제 4.09ms(33526 GFLOP/s)입니다. rocBLAS보다 더 좋습니다!
전체 커널 소스 코드는 여기에서 찾을 수 있습니다.
| Kernel # | Description | Time(ms) | Performance(GFLOPS) | Relative Performance to rocBLAS |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
| Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7% |
| Kernel 5 | LDS Utilization Optimization | 4.0994 | 33526.6 | 109.8 % |
우리는 VALU 활용도를 계속 증가시키고 있으며, 이제 우리 커널은 레지스터 사용량이 두 배가 되었습니다(레지스터 공간 요구 사항이 두 배가 되었기 때문에 당연한 일입니다). 점유율은 낮지만, VALU 단위를 더 잘 활용하고 있기 때문에 전반적인 성능이 더 좋습니다.

ISA를 살펴보면 이제 30사이클 미만의 작은 LDS 잠복기가 있으며, 그 대부분은 숨겨져 있습니다.

좋습니다. 커널은 rocBLAS보다 성능이 좋지만, dual_fmac 명령어를 사용하고 있기 때문에 성능이 예상만큼 높지 않습니다.
이 시점에서 여러 최적화를 시도했지만 HIP 컴파일러가 원하는 코드를 생성하도록 하는 데 어려움을 겪었습니다. C++ 코드를 약간만 변경해도 생성된 ISA가 크게 변경되어 최적화 작업이 매우 어려웠습니다. 이는 특히 컴파일러가 명시적 종속성이 부족하여 명령어를 잘못된 위치로 옮기는 인라인 어셈블리에서 문제가 되었습니다. 또한 특정 명령어에 특정 VGPR을 수동으로 할당할 방법이 없습니다.
이러한 문제 때문에 ISA 수준에서 직접 최적화하기로 했고, 이는 다음 단계에서 집중할 것입니다.
RGP를 살펴보면 내부 루프에서 여전히 한 가지가 궁금합니다. HIP 컴파일러는 dual_fmac 명령어를 독점적으로 사용하지 않습니다. 항상 몇 개의 단일 FMA 명령어가 섞여 있습니다. 또 다른 문제는 모든 v_dual_fmac 명령어의 최소 대기 시간이 2~3사이클이라는 것입니다. 이것이 중요하지 않은 것처럼 보일 수도 있지만, 모든 명령어에 걸쳐 누적되며 현재 실행 속도에서는 전반적인 성능에 영향을 미칩니다.
Kernel 6 : VALU optimization
다음 최적화에 들어가기 전에 ISA를 직접 수정할 수 있어야 합니다. 그러기 위해 이제 모듈 관리 API를 사용하여 미리 컴파일된 커널 코드를 로드할 수 있습니다. 물론 아이디어는 C++에서 커널의 ISA를 한 번 생성한 다음 추가 버전에 대해 ISA를 반복하는 것입니다.
그러기 위해 현재 C++ 커널에서 ISA 소스 파일을 추출하고 hip에 hsaco 바이너리 형식을 빌드하도록 요청해야 합니다.
hipcc --genco --offload-arch=gfx1100 kernel5_lds_optim.cpp -mcumode --save-temps -o tmp.hsaco |
--save-temps parameter를 사용하면 ISA가 포함된 중간 .s 파일에 액세스할 수 있습니다.
HIP은 다음 파일을 생성해야 합니다.
kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.bc kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.hipi kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.o kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.out kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.out.resolution.txt kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.s |
우리가 선택한 것은 kernel5_lds_optim-hip-amdgcn-amd-amdhsa-gfx1100.s입니다.
이제 우리는 이 파일을 수정의 기초로 삼고 다음 명령을 사용하여 조립할 수 있습니다.
hipcc -target amdgcn-amd-amdhsa -mcpu=gfx1100 -mcumode -c kernel_modified.s -o kernel.o ld.lld -shared kernel.o -o kernel.hsaco |
kernel.hsaco file은 HIP의 모듈 관리 API를 사용하여 런타임에 로드할 수 있습니다.
SA에 대한 직접 제어는 마이크로 벤치마킹에 유용하며, 예상치 못한 컴파일러 최적화에 대한 걱정 없이 성능 평가를 위한 코드를 계측하는 것을 더 쉽게 해줍니다.
예를 들어, 내부 루프에서 dual_fmac 명령어를 32번 복제하여 인위적으로 VALU에 바인딩될 수 있는지 확인해 보았습니다. 그러나 VALU 사용률은 75%를 초과할 수 없다는 것이 밝혀졌습니다!

다음으로 시도한 것은 단일 작업 그룹을 시작하고 단일 웨이브를 실행하는 것입니다. 이 2-3클럭 지연은 여전히 존재하므로 이는 이러한 dual_fmac 명령어의 VGPR 배포에서 비롯된 것입니다.
좋아요, 그럼 이 이중 명령어를 자세히 살펴보고 이에 대해 뭔가 할 수 있는지 알아보겠습니다. 이중 명령어는 다음과 같은 형태입니다.
OpCodeX DSTX, SRCX0, SRCX1 :: OpCodeY DSTY, SRCY0, SRCY1
우리의 경우에는 :
v_dual_fmac_f32 DSTX, SRCX0, SRCX1 :: v_dual_fmac_f32 DSTY, SRCY0, SRCY1
두 명령어는 동시에 실행되므로, 하나는 VGPR을 읽고 다른 하나는 같은 VGPR을 쓰더라도 두 명령어 사이에 경쟁이 없습니다. '읽기'는 이전 값을 가져옵니다.
이러한 명령어를 사용하려면 여러 가지 제약이 있습니다. 즉,
- 명령어는 서로 독립적이어야 합니다.
- SRCX0과 SRCY0은 서로 다른 VGPR 뱅크를 사용해야 합니다.
- 대상 VGPR : 하나는 짝수이고 다른 하나는 홀수여야 합니다.
- VSRCX1과 VSRCY1은 서로 다른 뱅크를 사용해야 합니다.
게다가 RDNA 3 프로그래밍 가이드는 다음과 같이 명시합니다.
- VGPR 뱅크는 4개(SRC[1:0]으로 인덱싱됨)가 있으며, 각 뱅크에는 캐시가 있습니다.
- 각 캐시에는 3개의 읽기 포트가 있습니다. 하나는 SRC0에, 하나는 SRC1에, 하나는 SRC2에 전용됩니다.
- 캐시는 3개를 모두 한 번에 읽을 수 있지만, 두 개의 SRC0(또는 SRC1/2)을 한 번에 읽을 수는 없습니다.
- FMAC_F32는 SRC2를 대상 피연산자로 사용합니다.
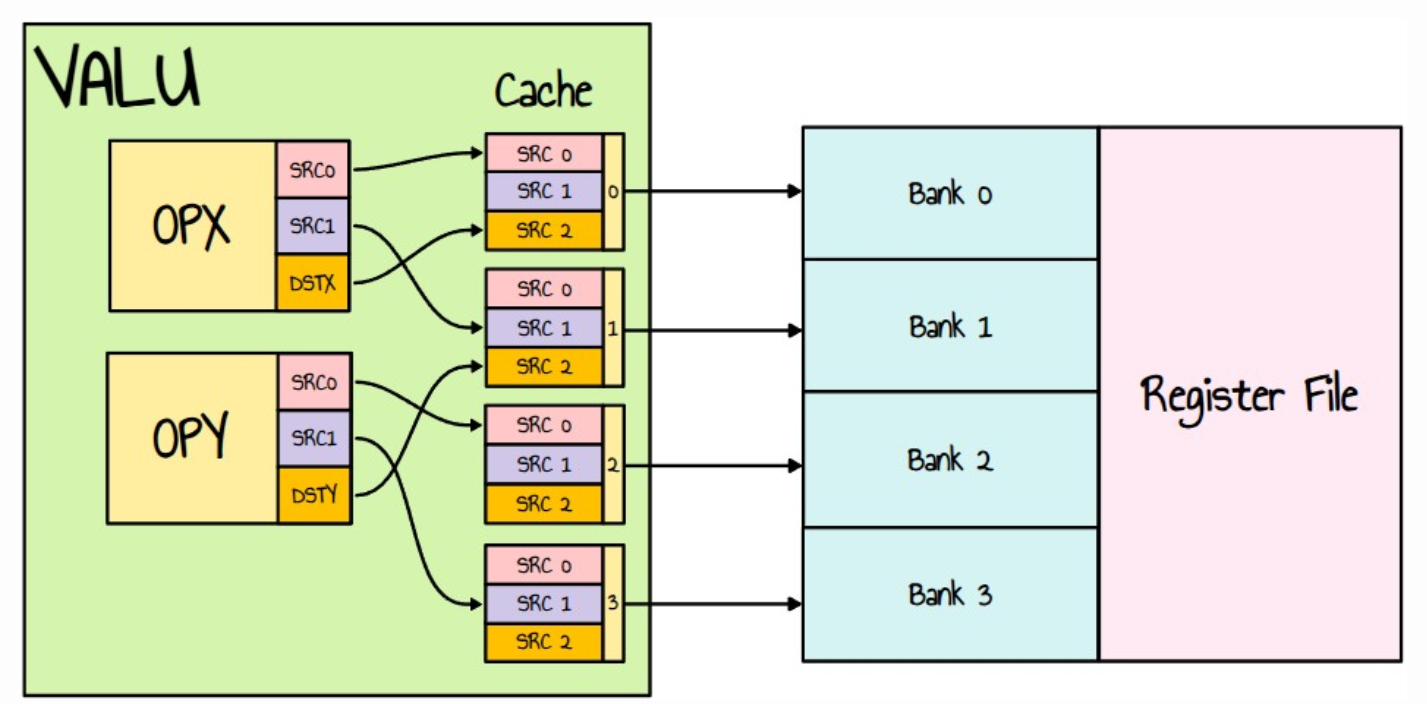

레지스터 X의 뱅크 번호는 X%4로 주어집니다.
예를 들면 :
v_dual_fmac_f32 v10, v189, v207 :: v_dual_fmac_f32 v9, v190, v20
FMAC Bank2, Bank1, Bank3 :: FMAC Bank1, Bank2, Bank0
이 명령어를 사용하면 4개의 다른 뱅크를 병렬로 읽고 다음 사이클에 뱅크 1과 2에 씁니다. 실제로는 동일한 피연산자를 사용하지 않는 경우 OPX와 OPY에서 모두 동일한 뱅크에서 읽을 수 있습니다. 예를 들어 SRCX0과 SRCY0이 서로 다른 뱅크를 사용하는 경우 이는 유효합니다.
v_dual_fmac_f32 v123, v139, v144 :: v_dual_fmac_f32 v114, v140, v143
FMAC Bank3, Bank3, Bank0 :: FMAC Bank2, Bank0, Bank3
두 명령어 모두 동일한 뱅크(0 및 3)를 읽습니다. 제가 보기에(제가 아는 한 ISA 가이드에는 포함되지 않음), 여기서 두 가지 일이 발생할 수 있습니다.
- VGPR 중 적어도 하나가 이미 캐시에 존재하여 명령어가 레지스터 파일에서 최대 하나의 값을 가져와야 합니다.
- VALU는 동일한 뱅크에서 두 개의 VGPR에 액세스해야 하므로 뱅크 충돌과 약간의 지연 시간이 발생합니다.
그 위에 다음 사이클에서 작성하더라도 작성하는 VGPR도 고려해야 합니다.
따라서 성공적으로 컴파일되는 유효한 VGPR 배포판이 있더라도 레지스터 뱅크 충돌이 발생하여 성능에 영향을 미칠 수 있습니다.
HIP 컴파일러가 생성한 내용을 살펴보겠습니다.
v_dual_fmac_f32 v127, v138, v144 :: v_dual_fmac_f32 v122, v139, v143
v_dual_fmac_f32 v128, v138, v145 :: v_dual_fmac_f32 v121, v139, v142 v_dual_fmac_f32 v123, v139, v144 :: v_dual_fmac_f32 v114, v140, v143 v_dual_fmac_f32 v124, v139, v145 :: v_dual_fmac_f32 v113, v140, v142 v_dual_fmac_f32 v115, v140, v144 :: v_dual_fmac_f32 v110, v141, v143 v_dual_fmac_f32 v116, v140, v145 :: v_dual_fmac_f32 v109, v141, v142 v_dual_fmac_f32 v111, v141, v144 :: v_dual_fmac_f32 v90, v138, v147 v_dual_fmac_f32 v112, v141, v145 :: v_dual_fmac_f32 v89, v138, v146 v_dual_fmac_f32 v91, v138, v148 :: v_dual_fmac_f32 v94, v139, v147 v_dual_fmac_f32 v92, v138, v149 :: v_dual_fmac_f32 v93, v139, v146 v_dual_fmac_f32 v95, v139, v148 :: v_dual_fmac_f32 v98, v140, v147 v_dual_fmac_f32 v96, v139, v149 :: v_dual_fmac_f32 v97, v140, v146 v_dual_fmac_f32 v99, v140, v148 :: v_dual_fmac_f32 v118, v141, v147 v_dual_fmac_f32 v100, v140, v149 :: v_dual_fmac_f32 v117, v141, v146 v_dual_fmac_f32 v119, v141, v148 :: v_dual_fmac_f32 v70, v138, v151 v_dual_fmac_f32 v120, v141, v149 :: v_dual_fmac_f32 v69, v138, v150 ;... |
첫 번째 명령어에 대한 뱅크와 캐시 상태를 모두 분석하면 다음과 같은 결과를 얻습니다.
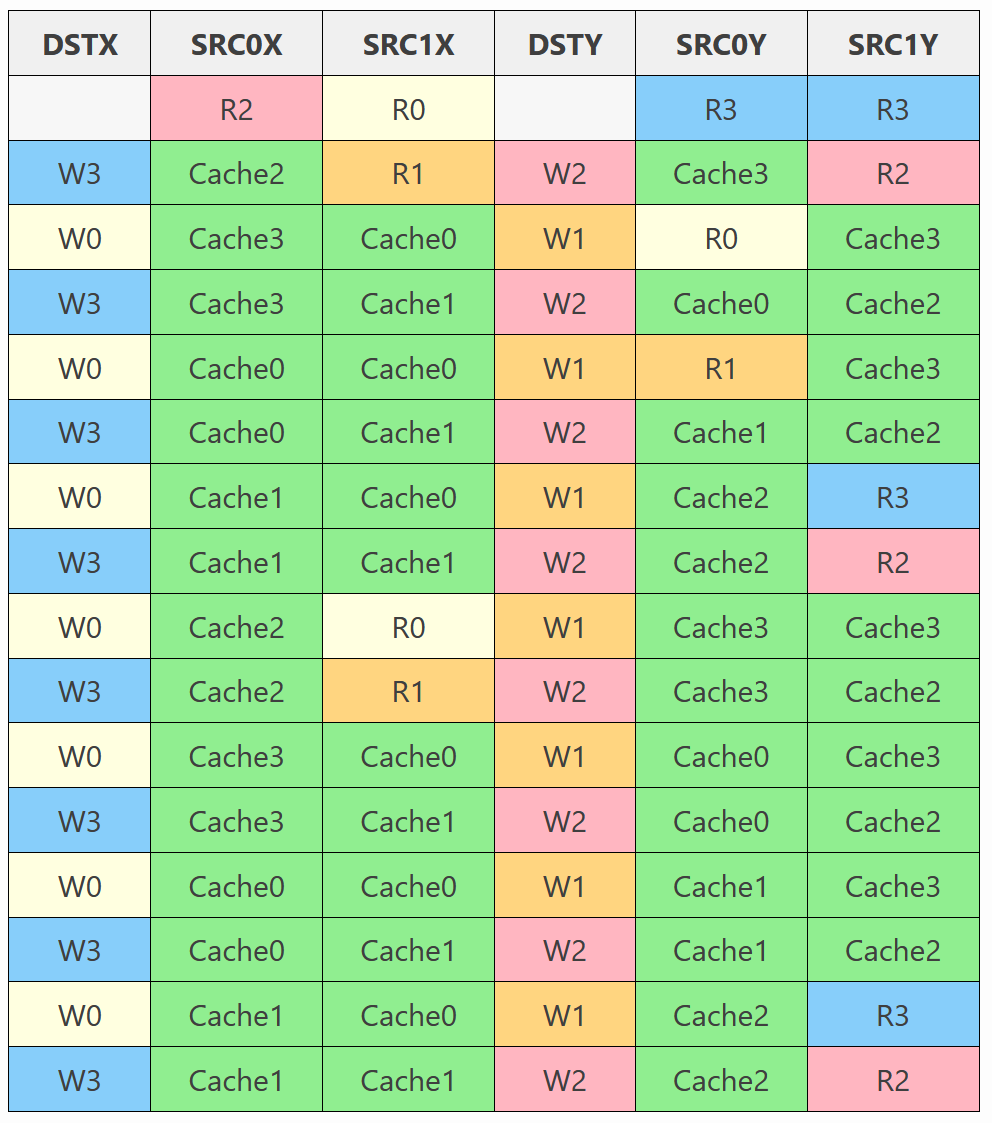
- R{k}는 우리가 뱅크 k에서 읽는다는 것을 의미합니다.
- W{k}는 우리가 뱅크 k에 쓰는 것을 의미합니다.
- Cache{k}는 우리가 뱅크 k와 연관된 캐시 중 하나에서 읽는 것을 의미합니다.
쓰기는 1클럭 지연으로 수행된다고 가정했는데, 이것이 DSTX와 DSTY의 첫 번째 행이 비어 있는 이유입니다.
컴파일러가 소량의 데이터만 읽기 때문에 캐시를 재사용하는 데 매우 효과적이라는 것을 알 수 있습니다. 그러나 액세스 패턴은 시간이 지남에 따라 일관되지 않으며 종종 동일한 뱅크를 두 번 이상 사용합니다.
VGPR 뱅크 측면에서 다양한 액세스 패턴에 따라 RGP에 표시되는 대기 시간을 이해하기 위해 마이크로 벤치마크를 만들기 시작했습니다. 그러나 이는 기본 아키텍처의 복잡성으로 인해 매우 복잡한 것으로 밝혀졌습니다.
여기에 너무 많은 시간을 할애하는 대신 다음 원칙에 따라 구현을 설계하려고 했습니다.
- 모든 VGPR 뱅크에 연속 패턴으로 쓰기
- 명령어당 읽는 다양한 VGPR 뱅크 수를 최대화
- VGPR 캐시 사용을 최대화
- 단일하고 일관된 액세스 패턴을 유지하고 가능한 한 대칭을 목표로 합니다.
좋은 소식은 내부 루프의 반복 횟수가 상당히 높기 때문에 출력 행렬 C의 정렬 제약 조건을 무시할 수 있다는 것입니다. 즉, 축적 단계 동안 레지스터 할당을 자유롭게 섞고 메모리에 쓰기 전에 한 번만 재정렬할 수 있습니다. 이렇게 하면 더 이상 연속 메모리 위치와 연속 레지스터 간에 직접 매핑을 유지할 필요가 없으므로 제약 조건 하나를 효과적으로 제거할 수 있습니다. 이것이 HIP 컴파일러가 dual_fmac 명령어만 사용하는 데 어려움을 겪었던 이유일 수 있습니다(global_store_b128에 의한 행렬 C_reg를 C에 쓰려면 4개의 연속 VGPR이 필요함)
커널 4부터 내부 루프는 A의 열에 있는 8개 요소와 B의 행에 있는 16개 요소 간의 곱셈을 수행하는 것으로 구성됩니다. A와 B가 모두 4개의 다른 VGPR 뱅크에 연속적으로 분포되어 있다고 가정할 수 있습니다. 다음과 같습니다.
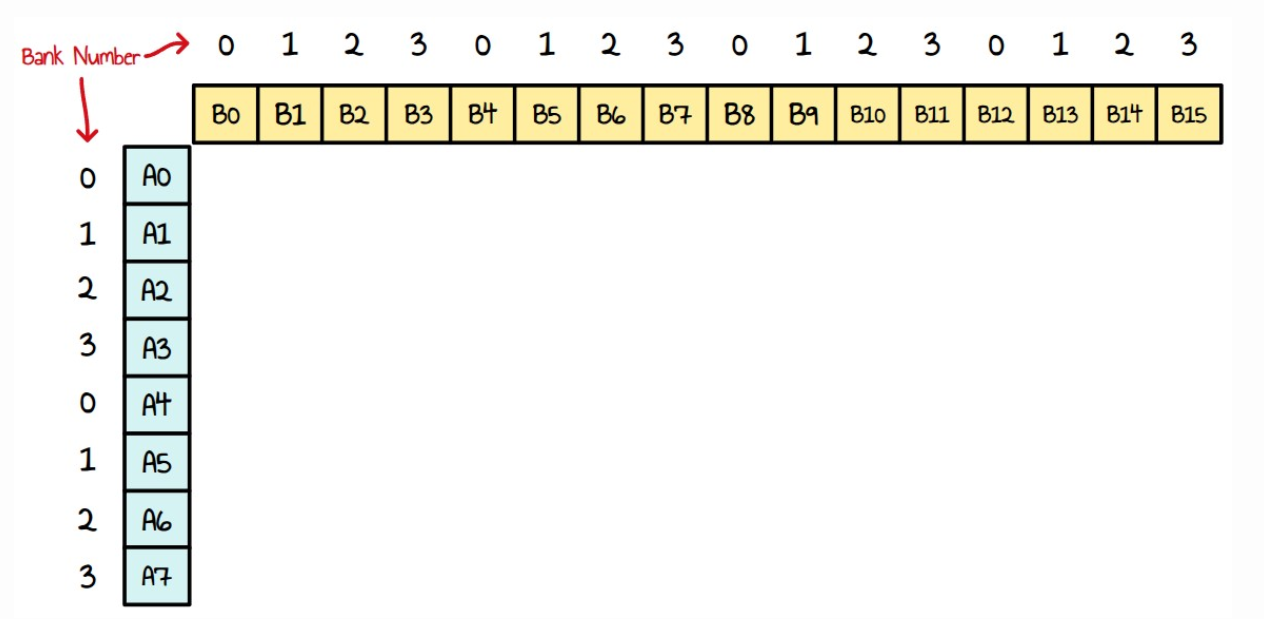
단순성을 위해 지금부터는 8x4 타일에서만 알고리즘을 표현하겠습니다. 순진한 접근 방식은 이와 같이 작은 대각선을 이동하여 이중 명령어를 만드는 것입니다. 이렇게 하면 SRC0와 SRC1이 서로 다른 뱅크를 사용하도록 합니다.

셀 번호는 명령어 인덱스를 나타냅니다.
이중 이슈 명령어만 사용하는 것이 완벽하게 가능하다는 것을 알 수 있지만, 그 중 일부는 동일한 뱅크를 여러 번 사용하고 있습니다. 이는 우리가 피하고 싶었던 것입니다. 이를 없애는 한 가지 방법은 A와 B를 겹치지 않는 뱅크 세트에 저장하는 것입니다. 예를 들어 B는 뱅크 0-1에만, A는 뱅크 2-3에만 저장합니다. 이 경우의 문제점은 4개의 연속된 VGPR을 대상으로 하기 때문에 더 이상 ds_load_b128 명령어를 사용할 수 없다는 것입니다. 따라서 지금처럼 6개의 ds_load_b128 명령어를 사용하는 대신 12개의 ds_load_b64를 사용하게 됩니다. 변경으로 인한 성능 향상이 충분히 좋다면 문제가 되지 않습니다.

모두 녹색! 하지만 캐시 사용과 읽기 패턴을 살펴보면 다음과 같습니다.
우리는 A의 값을 잘 재사용하지만 명령어 8은 두 번 읽습니다. 그러나 아래의 자세한 표에서 읽기 패턴을 살펴보면 대부분 뱅크 0과 뱅크 1에서 읽고 명령어 Y(원하는 만큼 대칭적이지 않음)에서 읽는 것을 알 수 있습니다.
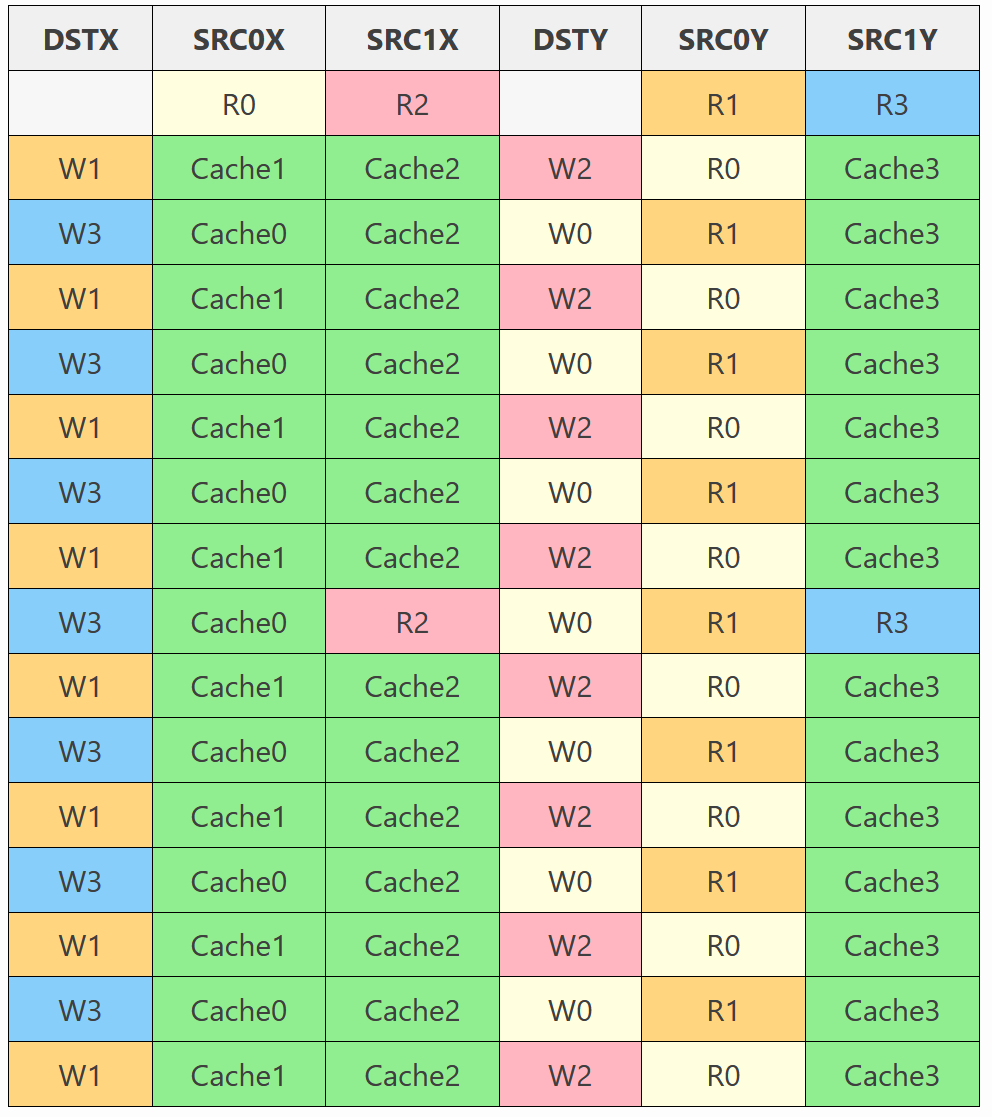
A 값만을 반복하는 대신 A와 B를 모두 반복하면서 명령어 X와 Y 사이에서 레지스터를 바꿔 캐시 사용량을 극대화할 수 있습니다.

자세한 뷰를 보면, 이제 우리는 멋지고 대칭적인 액세스 패턴을 가지고 있습니다. 명령어 X와 Y는 모두 레지스터 파일에서 같은 양의 데이터를 읽고, 우리는 4개의 뱅크를 순차적으로 반복합니다(뱅크 0과 1만이 아닙니다)

이제 새로운 액세스 패턴에 만족합니다. 이 변경 사항을 코드에 어떻게 적용할 수 있을까요? 단계는 다음과 같습니다.
- 현재 코드에서 사용하는 VGPR을 나열합니다.
- 이러한 VGPR을 재배포하여 다음을 수행합니다.
- C_reg가 연속된 뱅크 세그먼트를 차지하도록 합니다.
- A_col 및 B_row를 겹치지 않는 뱅크 세트(예: 뱅크 0-1 및 뱅크 2-3)에 할당합니다.
- A_col 및 B_row에 대한 LDS 로드를 다시 구현합니다.
- 내부 루프(128 v_dual_fmac 명령어)를 다시 작성합니다.
- 글로벌 메모리에 쓰기 위한 기존 코드와의 호환성을 유지하기 위해 루프 뒤에 VGPR 매핑을 복원합니다.
사용된 VGPR을 리스트
ds_load_b128 명령어부터 시작해 보겠습니다.
ds_load_b128 v[184:187], v183 ds_load_b128 v[188:191], v183 offset:64 ds_load_b128 v[192:195], v204 ds_load_b128 v[196:199], v204 offset:128 ds_load_b128 v[200:203], v204 offset:256 ds_load_b128 v[204:207], v204 offset:384 |
- v183은 As의 LDS 주소입니다.
- VGPR [184, 191]은 As를 저장하는 데 사용됩니다.
- v204는 B의 LDS 주소입니다.
- VGPR [192, 207]은 B를 저장하는 데 사용됩니다.
행렬 C_reg는 다음 범위에 걸쳐 분포합니다: [2,117], [120, 124], [126, 129], [131, 133]
VGPR 재분배
C_reg에 대한 VGPR 할당이 이미 필요한 것에 가까운 것으로 나타났습니다. 모든 128개 VGPR이 뱅크 0-3에 순차적으로 할당되도록 하려면 여분의 뱅크 2 VGPR만 추가하면 됩니다.
이는 C_reg에 대한 초기화 코드(모든 값을 0.0으로 설정)와의 호환성을 유지할 수 있으므로 좋은 소식입니다.
C_reg에 대한 새로운 할당: [2,117], [120, 124], [126, 129], [131, 133], [214]
A_col 및 B_row의 경우 B_row가 뱅크 0-1만 사용하므로 추가 레지스터도 할당해야 합니다.
A_col 및 B_row에 대한 새로운 할당 :
- A_col: [186, 187], [190, 191], [194, 195], [198, 199] (뱅크 2-3)
- B_row: [184, 185], [188, 189], [192, 193], [196, 197], [200, 201], [204, 205], [208, 209], [212, 213] (뱅크 0-1)
Re-wirte LDS Loads
A에서 A_col을 로드하기 위한 새로운 코드 :
;A on bank 2-3 ds_load_b64 v[186:187], v183 ds_load_b64 v[190:191], v183 offset: 8 ds_load_b64 v[194:195], v183 offset: 64 ds_load_b64 v[198:199], v183 offset: 72 |
Bs에서 B_row 로딩:
;B on bank 0-1 ds_load_b64 v[184:185], v202 ds_load_b64 v[188:189], v202 offset: 8 ds_load_b64 v[192:193], v202 offset: 128 ds_load_b64 v[196:197], v202 offset: 136 ds_load_b64 v[200:201], v202 offset: 256 ds_load_b64 v[204:205], v202 offset: 264 ds_load_b64 v[208:209], v202 offset: 384 ds_load_b64 v[212:213], v202 offset: 392 |
v183과 v202는 LDS 메모리에서 A와 B의 주소를 보관하는 새로운 VGPR입니다.
dual_fmas를 다시 작성합니다.
그러면 내부 루프를 v_dual_fmac로만 작성할 수 있습니다.
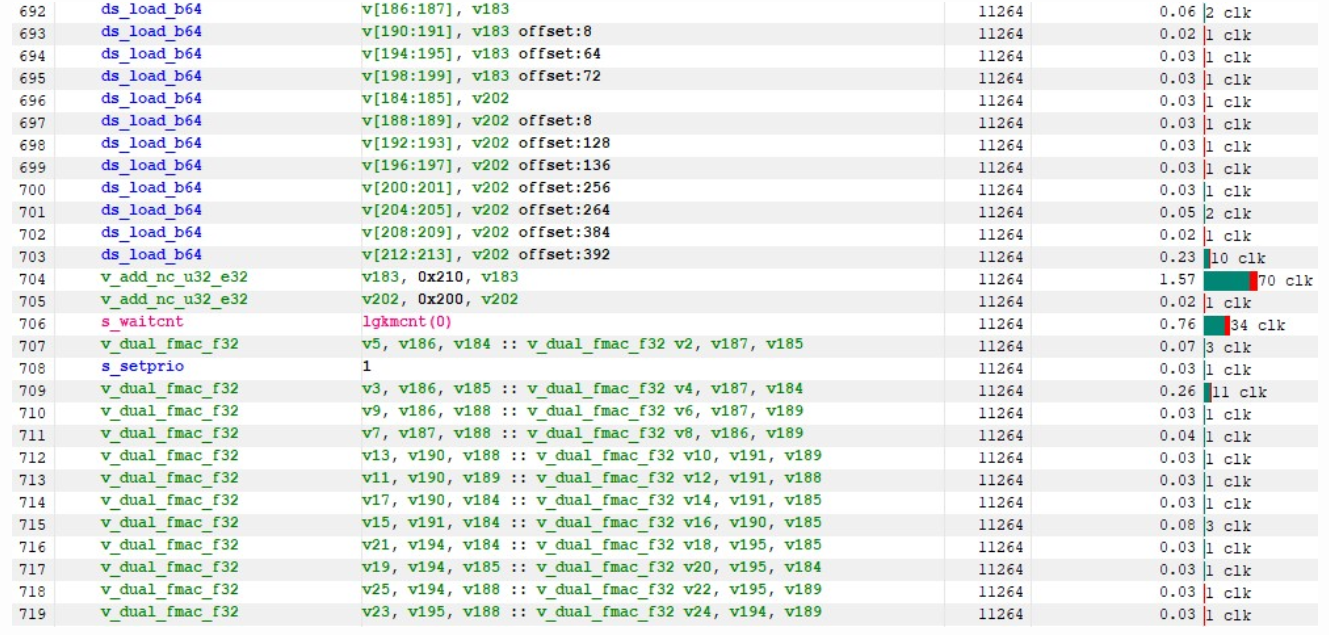
v_dual_fmac_f32 v5, v186, v184 :: v_dual_fmac_f32 v2, v187, v185 v_dual_fmac_f32 v3, v186, v185 :: v_dual_fmac_f32 v4, v187, v184 v_dual_fmac_f32 v9, v186, v188 :: v_dual_fmac_f32 v6, v187, v189 v_dual_fmac_f32 v7, v187, v188 :: v_dual_fmac_f32 v8, v186, v189 v_dual_fmac_f32 v13, v190, v188 :: v_dual_fmac_f32 v10, v191, v189 v_dual_fmac_f32 v11, v190, v189 :: v_dual_fmac_f32 v12, v191, v188 v_dual_fmac_f32 v17, v190, v184 :: v_dual_fmac_f32 v14, v191, v185 v_dual_fmac_f32 v15, v191, v184 :: v_dual_fmac_f32 v16, v190, v185 v_dual_fmac_f32 v21, v194, v184 :: v_dual_fmac_f32 v18, v195, v185 v_dual_fmac_f32 v19, v194, v185 :: v_dual_fmac_f32 v20, v195, v184 v_dual_fmac_f32 v25, v194, v188 :: v_dual_fmac_f32 v22, v195, v189 v_dual_fmac_f32 v23, v195, v188 :: v_dual_fmac_f32 v24, v194, v189 v_dual_fmac_f32 v29, v198, v188 :: v_dual_fmac_f32 v26, v199, v189 v_dual_fmac_f32 v27, v198, v189 :: v_dual_fmac_f32 v28, v199, v188 v_dual_fmac_f32 v33, v198, v192 :: v_dual_fmac_f32 v30, v199, v193 v_dual_fmac_f32 v31, v199, v192 :: v_dual_fmac_f32 v32, v198, v193 v_dual_fmac_f32 v37, v186, v192 :: v_dual_fmac_f32 v34, v187, v193 v_dual_fmac_f32 v35, v186, v193 :: v_dual_fmac_f32 v36, v187, v192 v_dual_fmac_f32 v41, v186, v196 :: v_dual_fmac_f32 v38, v187, v197 v_dual_fmac_f32 v39, v187, v196 :: v_dual_fmac_f32 v40, v186, v197 v_dual_fmac_f32 v45, v190, v196 :: v_dual_fmac_f32 v42, v191, v197 v_dual_fmac_f32 v43, v190, v197 :: v_dual_fmac_f32 v44, v191, v196 v_dual_fmac_f32 v49, v190, v192 :: v_dual_fmac_f32 v46, v191, v193 v_dual_fmac_f32 v47, v191, v192 :: v_dual_fmac_f32 v48, v190, v193 v_dual_fmac_f32 v53, v194, v192 :: v_dual_fmac_f32 v50, v195, v193 v_dual_fmac_f32 v51, v194, v193 :: v_dual_fmac_f32 v52, v195, v192 v_dual_fmac_f32 v57, v194, v196 :: v_dual_fmac_f32 v54, v195, v197 v_dual_fmac_f32 v55, v195, v196 :: v_dual_fmac_f32 v56, v194, v197 v_dual_fmac_f32 v61, v198, v196 :: v_dual_fmac_f32 v58, v199, v197 v_dual_fmac_f32 v59, v198, v197 :: v_dual_fmac_f32 v60, v199, v196 v_dual_fmac_f32 v65, v198, v200 :: v_dual_fmac_f32 v62, v199, v201 v_dual_fmac_f32 v63, v199, v200 :: v_dual_fmac_f32 v64, v198, v201 v_dual_fmac_f32 v69, v186, v200 :: v_dual_fmac_f32 v66, v187, v201 v_dual_fmac_f32 v67, v186, v201 :: v_dual_fmac_f32 v68, v187, v200 v_dual_fmac_f32 v73, v186, v204 :: v_dual_fmac_f32 v70, v187, v205 v_dual_fmac_f32 v71, v187, v204 :: v_dual_fmac_f32 v72, v186, v205 v_dual_fmac_f32 v77, v190, v204 :: v_dual_fmac_f32 v74, v191, v205 v_dual_fmac_f32 v75, v190, v205 :: v_dual_fmac_f32 v76, v191, v204 v_dual_fmac_f32 v81, v190, v200 :: v_dual_fmac_f32 v78, v191, v201 v_dual_fmac_f32 v79, v191, v200 :: v_dual_fmac_f32 v80, v190, v201 v_dual_fmac_f32 v85, v194, v200 :: v_dual_fmac_f32 v82, v195, v201 v_dual_fmac_f32 v83, v194, v201 :: v_dual_fmac_f32 v84, v195, v200 v_dual_fmac_f32 v89, v194, v204 :: v_dual_fmac_f32 v86, v195, v205 v_dual_fmac_f32 v87, v195, v204 :: v_dual_fmac_f32 v88, v194, v205 v_dual_fmac_f32 v93, v198, v204 :: v_dual_fmac_f32 v90, v199, v205 v_dual_fmac_f32 v91, v198, v205 :: v_dual_fmac_f32 v92, v199, v204 v_dual_fmac_f32 v97, v198, v208 :: v_dual_fmac_f32 v94, v199, v209 v_dual_fmac_f32 v95, v199, v208 :: v_dual_fmac_f32 v96, v198, v209 v_dual_fmac_f32 v101, v186, v208 :: v_dual_fmac_f32 v98, v187, v209 v_dual_fmac_f32 v99, v186, v209 :: v_dual_fmac_f32 v100, v187, v208 v_dual_fmac_f32 v105, v186, v212 :: v_dual_fmac_f32 v102, v187, v213 v_dual_fmac_f32 v103, v187, v212 :: v_dual_fmac_f32 v104, v186, v213 v_dual_fmac_f32 v109, v190, v212 :: v_dual_fmac_f32 v106, v191, v213 v_dual_fmac_f32 v107, v190, v213 :: v_dual_fmac_f32 v108, v191, v212 v_dual_fmac_f32 v113, v190, v208 :: v_dual_fmac_f32 v110, v191, v209 v_dual_fmac_f32 v111, v191, v208 :: v_dual_fmac_f32 v112, v190, v209 v_dual_fmac_f32 v117, v194, v208 :: v_dual_fmac_f32 v114, v195, v209 v_dual_fmac_f32 v115, v194, v209 :: v_dual_fmac_f32 v116, v195, v208 v_dual_fmac_f32 v121, v194, v212 :: v_dual_fmac_f32 v122, v195, v213 v_dual_fmac_f32 v123, v195, v212 :: v_dual_fmac_f32 v120, v194, v213 v_dual_fmac_f32 v129, v198, v212 :: v_dual_fmac_f32 v126, v199, v213 v_dual_fmac_f32 v127, v198, v213 :: v_dual_fmac_f32 v124, v199, v212 v_dual_fmac_f32 v133, v198, v184 :: v_dual_fmac_f32 v214, v199, v185 v_dual_fmac_f32 v131, v199, v184 :: v_dual_fmac_f32 v128, v198, v185 |
VGPR 매핑 복원
다음과 같이 임시 VGPR을 사용하여 전체 매핑을 복원합니다.
; v2 -> v128 & v128 -> v2 v_mov_b32 v200, v128 v_mov_b32 v128, v2 v_mov_b32 v2, v200 ; v128 -> v56 & v56 -> v128 v_mov_b32 v200, v56 v_mov_b32 v56, v2 v_mov_b32 v2, v200 ; v56 -> v46 & v46 -> v56 v_mov_b32 v200, v46 v_mov_b32 v46, v2 v_mov_b32 v2, v200 ; v46 -> v100 & v100 -> v46 v_mov_b32 v200, v100 v_mov_b32 v100, v2 v_mov_b32 v2, v200 ... |
이러한 변경을 용이하게 하기 위해 저는 ISA를 구문 분석하고, 이전 및 새 VGPR 배포판 간의 매핑을 추출하고, 필요한 모든 지침을 자동으로 생성하는 작은 C++ 프로그램을 작성했습니다.
이제 커널은 208개가 아닌 214개의 VGPR을 사용합니다. amdhsa.kernels 섹션의 .s 파일에서 이를 수정해야 합니다.
.vgpr_count: 214
전체 커널 소스 코드는 여기에서 찾을 수 있습니다.
이 커널의 성능은 3.63ms(37791.2 GFLOP/s)입니다.
| Kernel # | Description | Time(ms) | Performance(GFLOPS) | Relative Performance to rocBLAS |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
| Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7% |
| Kernel 5 | LDS Utilization Optimization | 4.0994 | 33526.6 | 109.8 % |
| Kernel 6 | VALU Utilization Optimization | 3.6368 | 37791.2 | 123.7 % |
우리의 VALU 활용도는 76.2%로 다시 상승했습니다(내부 루프의 32배인 75%보다 높음).
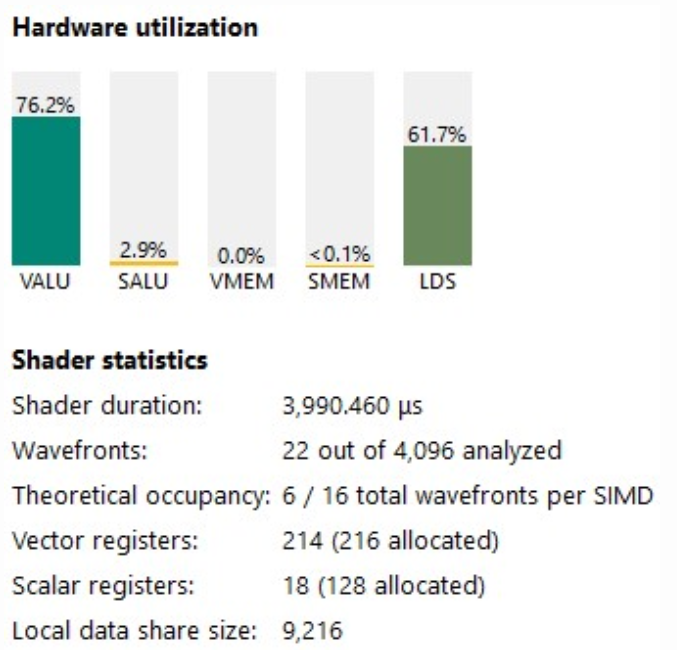
이 ISA를 살펴보면, 우리의 내부 루프는 v_dual_fmac 명령어로만 구성되어 있으며, 각각은 1주기 지연 시간을 갖습니다. 아름답네요!

또한 분기에서 루프의 끝에서 많은 사이클이 낭비되는 것을 볼 수 있습니다. 다음 커널에서 이를 최적화해 보겠습니다.
Kernel 7 : Loop unrolling
이전에 C++ HIP 구현에서 내부 루프를 풀어보려고 했지만, 제대로 작동하지 않았습니다. 컴파일러가 LDS12에서 더 많은 값을 미리 가져오면서 커널이 너무 커졌고, 성능은 변함없이 유지되었습니다.13
이제 매우 효율적인 루프와 ISA에 대한 완전한 제어권을 확보했으니, 더 나은 결과를 얻을 수 있을 것입니다. 이 단계에서는 커널 6에서 추가된 코드를 여덟 번 복제하고 루프 메커니즘을 제거하겠습니다.
s_cmpk_lg_i32 s14, 0x1000 ; Remove this line at the beginning of the loop s_waitcnt lgkmcnt(0) v_dual_fmac_f32 ... v_dual_fmac_f32 ... s_cbranch_scc1 .LBB0_9 ; Remove this line at the end of the loop |
데이터 로드와 곱셈 연산을 8회 중복 실행하되, 각 반복마다 주소를 증가시켜야 합니다.
v_add_nc_u32_e32 v183, 0x210, v183 ; B : 0x210 = (128+4)*4 v_add_nc_u32_e32 v202, 0x200, v202 ; A : 0x200 = (128)*4 |
전체 커널 소스 코드는 여기에서 확인할 수 있습니다.
이 커널의 성능은 3.33ms(41255.6GFLOPS/s)입니다.
| Kernel # | Description | Time (ms) |
Performance (GFLOPS) |
Relative Performace to rocBLAS |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
| Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7% |
| Kernel 5 | LDS Utilization Optimization | 4.0994 | 33526.6 | 109.8 % |
| Kernel 6 | VALU Utilization Optimization | 3.6368 | 37791.2 | 123.7 % |
| Kernel 7 | Unroll inner loop | 3.3314 | 41255.6 | 135.1 % |
VALU 활용도는 현재 80%를 넘었습니다.
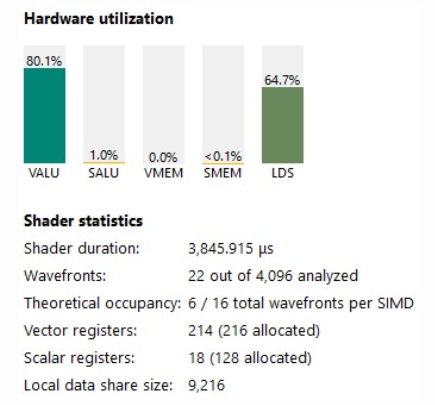
인스트럭션 타이밍도 매우 좋아 보입니다.
- v_dual_fmac은 평균 1 클럭 지연 시간을 갖습니다.
- ds_loads는 평균 1 클럭 지연 시간을 갖습니다.
- lds 대기 시간은 34사이클에 불과하며, 대부분은 VALU 연산에 의해 숨겨집니다.
그렇다면 왜 더 빠르지 않을까요?
RGP의 총 지연 시간(Clk)을 살펴보면, 가장 큰 원인은 배리어 대기입니다. 바로 앞의 s_waitcnt는 글로벌 메모리 로드 대기입니다.

LDS에 쓰기 전에 스레드를 동기화해야 하므로 이 배리어를 제거할 수 없습니다. 하지만 생성된 코드에서 전역 메모리 로드를 살펴보면, 해당 작업에 할당된 큰 코드 세그먼트(128줄)가 있음을 알 수 있습니다.
이전에는 몰랐는데, 지연 시간이 부분적으로 감춰져 있음에도 불구하고 단일 로드에 대한 누적 지연 시간은 약 130만 클럭입니다. 16개의 서로 다른 로드(각 행렬에 8개씩)를 수행한다고 가정하면, 여기서는 2천만 클럭의 지연 시간이 발생합니다!
다음 커널에서 이 문제를 어떻게 개선할 수 있는지 살펴보겠습니다.
Kernel 8 : Batched GMEM loads
좋습니다. HIP가 우리를 위해 생성한 내용을 살펴보겠습니다(더 나은 가독성을 위해 s_delay_alu 명령어를 제거했습니다)
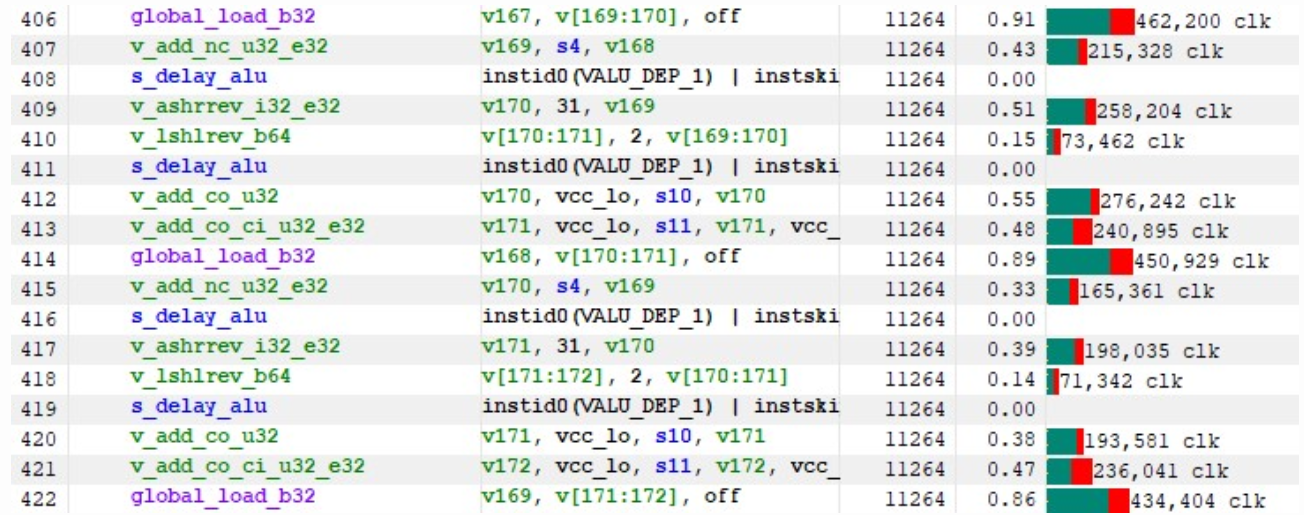
v_add_nc_u32_e32 v169, s4, v168 v_ashrrev_i32_e32 v170, 31, v169 v_lshlrev_b64 v[170:171], 2, v[169:170] v_add_co_u32 v170, vcc_lo, s10, v170 v_add_co_ci_u32_e32 v171, vcc_lo, s11, v171, vcc_lo global_load_b32 v168, v[170:171], off v_add_nc_u32_e32 v170, s4, v169 v_ashrrev_i32_e32 v171, 31, v170 v_lshlrev_b64 v[171:172], 2, v[170:171] v_add_co_u32 v171, vcc_lo, s10, v171 v_add_co_ci_u32_e32 v172, vcc_lo, s11, v172, vcc_lo global_load_b32 v169, v[171:172], off |
여기서 s[10:11]은 행렬 B의 주소를 저장합니다. 각 global_load_b32에 대해 컴파일러는 이전 반복(여기서는 v170 및 v171)의 VGPR을 사용하여 읽기 오프셋을 계산합니다. 이는 몇 가지 이유로 이상적이지 않습니다.
- 모든 global_load는 먼저 VALU 연산을 완료해야 합니다. 이 VALU는 FMA 연산을 수행하는 다른 파동에서 사용되지 않습니다.
- global_load 연산 간의 종속성은 불필요한 지연 시간을 발생시킵니다.
- GMEM 상태에서 너무 많은 사이클을 소비하면 동일한 SIMD의 여러 파동이 동시에 해당 상태에 있을 가능성이 높아져 VALU 작업이 효과적으로 줄어듭니다.
따라서 이상적으로는 이 128줄짜리 코드 섹션을 16줄로 줄이는 것이 좋습니다.
global_load_b32 v169, v[171:172], off global_load_b32 v170, v[173:174], off global_load_b32 v171, v[175:176], off .... |
하지만 이렇게 하려면 추가 VGPR을 유지해야 하고, 메모리 주소 업데이트에 VALU 명령어를 사용해야 할 가능성도 있습니다. 이미 214개의 VGPR을 사용하고 있다는 점을 고려하면 이는 분명히 실현 가능하지 않습니다.
그럼에도 불구하고 SGPR 예산은 상당히 넉넉하며, RDNA3 프로그래밍 가이드에 따르면 global_load 명령어는 SGPR을 기본 주소 지정에 사용할 수 있습니다.
global_load_b32 v171, v214, s[10:11] |
v214는 이제 바이트 단위의 오프셋입니다. s[10:11]은 메모리의 64비트 주소입니다.
따라서 16개의 로드에 필요한 모든 주소를 미리 계산한 후 루프에서 오프셋만 한 번 증가시킬 수 있습니다. 이렇게 하면 오프셋을 처리하기 위해 16*2 SGPR과 2개의 VGPR이 추가로 필요합니다.
ISA를 살펴보면 다음과 같습니다.
- s[0:1]에는 커널 매개변수의 주소가 포함되어 있습니다.
- s14와 s15에는 blockIdx가 포함되어 있습니다.
- v0은 threadIdx.x입니다.
필요한 기본 주소를 계산하는 데 필요한 것은 이것뿐입니다.
먼저, 처음 128바이트를 로드하여 행렬 A와 B의 주소를 s[20:21]과 s[22:23]에 로드합니다.
s_load_b128 s[20:23], s[0:1], 0x0 ; Matrix A and B s_waitcnt lgkmcnt(0) |
행렬 B의 경우, s[24:39]에 미리 계산된 오프셋을 사용하여 기본 주소를 저장합니다. C++ 코드로 돌아가 보면, 각 오프셋은 strideReadB*N = BLOCK_SIZE / BN * N으로 구분되어 있으며, 이는 4096x4 = 0x4000바이트입니다.
s_add_u32 s24, s22, 0x0000 s_addc_u32 s25, s23, 0 s_add_u32 s26, s22, 0x4000 s_addc_u32 s27, s23, 0 s_add_u32 s28, s22, 0x8000 s_addc_u32 s29, s23, 0 s_add_u32 s30, s22, 0xc000 s_addc_u32 s31, s23, 0 s_add_u32 s32, s22, 0x10000 s_addc_u32 s33, s23, 0 s_add_u32 s34, s22, 0x14000 s_addc_u32 s35, s23, 0 s_add_u32 s36, s22, 0x18000 s_addc_u32 s37, s23, 0 s_add_u32 s38, s22, 0x1c000 s_addc_u32 s39, s23, 0 |
인덱스를 바이트 단위로 계산하려면 다음을 수행하면 됩니다.
; compute Matrix B offset s_lshl_b32 s19, s14, 7 ; BN * blockIdx.x v_add_nc_u32_e32 v203, s19, v0 ; index = BN * blockIdx.x + threadIdx.x v_lshlrev_b32_e32 v203,2, v203 ; offset = 4*index (to bytes offset) |
우리는 기본 주소에 s[40:55]를, 오프셋에 v215를 사용하여 행렬 A에 동일한 로직을 적용합니다.
s_add_u32 s40, s20, 0x0000 s_addc_u32 s41, s21, 0 s_add_u32 s42, s20, 0x40000 s_addc_u32 s43, s21, 0 s_add_u32 s44, s20, 0x80000 s_addc_u32 s45, s21, 0 s_add_u32 s46, s20, 0xc0000 s_addc_u32 s47, s21, 0 s_add_u32 s48, s20, 0x100000 s_addc_u32 s49, s21, 0 s_add_u32 s50, s20, 0x140000 s_addc_u32 s51, s21, 0 s_add_u32 s52, s20, 0x180000 s_addc_u32 s53, s21, 0 s_add_u32 s54, s20, 0x1c0000 s_addc_u32 s55, s21, 0 ; compute Matrix A offset s_lshl_b32 s19, s15, 19 ; 4096 * 128 * blockIdx.y v_lshrrev_b32_e32 v1, 3, v0 ; threadIdx.x / 8 v_lshlrev_b32_e32 v1, 12, v1 ; 4096 * (threadIdx.x/8) v_and_b32_e32 v215, 7, v0 ; threadIdx.x % 8 v_add_u32_e32 v215, v1, v215 ; index = 4096*(threadIdx.x/8) + threadIdx.x % 8 v_add_nc_u32_e32 v215, s19, v215 ; index += 4096*128*blockIdx.y v_lshlrev_b32_e32 v215,2, v215 ; offset = 4*index |
이제 메인 루프에서 128줄의 코드를 다음으로 바꿀 수 있습니다.
v_add_nc_u32_e32 v203, 0x20000, v203 v_add_nc_u32_e32 v215, 0x20, v215 global_load_b32 v167, v203, s[24:25] global_load_b32 v168, v203, s[26:27] global_load_b32 v169, v203, s[28:29] global_load_b32 v170, v203, s[30:31] global_load_b32 v171, v203, s[32:33] global_load_b32 v172, v203, s[34:35] global_load_b32 v173, v203, s[36:37] global_load_b32 v174, v203, s[38:39] global_load_b32 v175, v215, s[40:41] global_load_b32 v176, v215, s[42:43] global_load_b32 v177, v215, s[44:45] global_load_b32 v178, v215, s[46:47] global_load_b32 v179, v215, s[48:49] global_load_b32 v180, v215, s[50:51] global_load_b32 v181, v215, s[52:53] global_load_b32 v182, v215, s[54:55] |
수정된 커널은 이제 18개 대신 55개의 SGPR을 사용하고 214개 대신 216개의 VGPR을 사용합니다. 다른 RGP 캡처를 수행하면 전체 프로세스에 대한 지연 시간이 200만 클럭 사이클 미만으로 훨씬 더 좋아졌음을 알 수 있습니다.

몇 가지 실험을 해 본 결과, 이 16개의 부하를 내부 루프에 분산하는 것이 더 효율적이라는 것을 알게 되었습니다. 현재 저희 커널은 SIMD당 6개의 웨이브프런트를 실행합니다. 작업 그룹은 128개의 스레드(4개의 웨이브)로 구성되어 있으므로, 싱크스레드(syncthread)를 실행할 때마다 SIMD의 6개 웨이브 중 최소 2개가 GMEM 접근을 위해 경쟁하게 됩니다. 또한, 나머지 4개 웨이브 중 하나라도 동일한 상태에 있다면 더 많은 웨이브가 메모리 접근을 위해 경쟁할 수 있습니다.
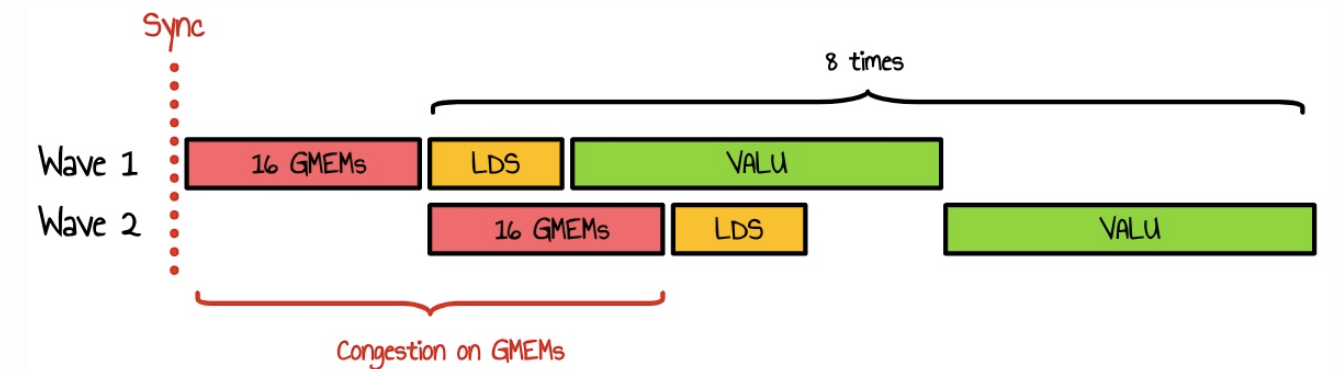
이러한 하중을 2개로 나누면 다음 다이어그램에서 볼 수 있듯이 파도가 겹칠 가능성이 줄어듭니다.
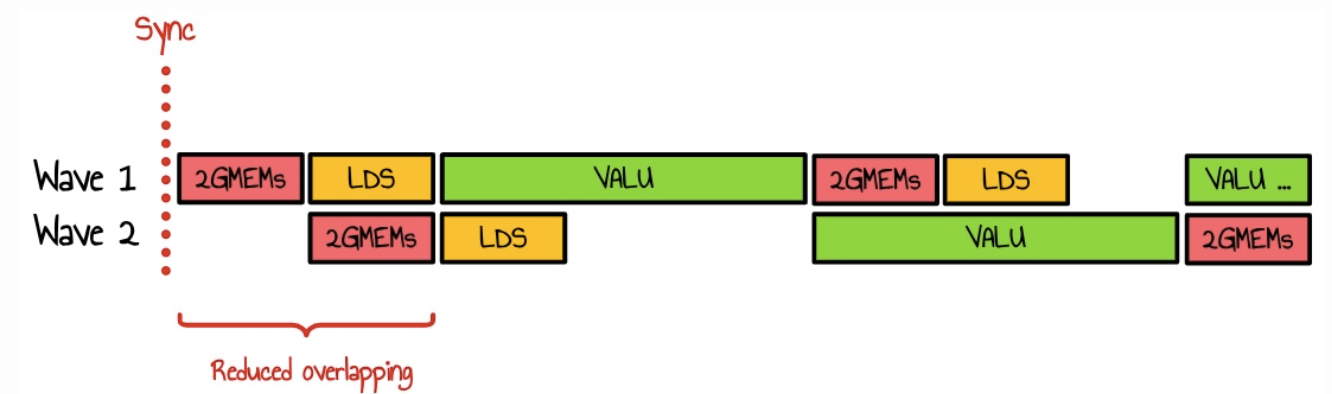
이 커널의 성능은 2.80ms(49047 GFLOPS/s)입니다. 이는 기존 rocBLAS 버전보다 60%, 기존 방식보다 거의 50배 빠른 속도입니다!
전체 커널 소스 코드는 여기에서 확인할 수 있습니다.
| Kernel # | Description | Time (ms) |
Performance (GFLOPS) |
Relative Performance to rocBLAS |
| Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % |
| Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % |
| Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |
| Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |
| Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7 % |
| Kernel 5 | LDS Utilization Optimization | 4.0994 | 33526.6 | 109.8 % |
| Kernel 6 | VALU Utilization Optimization | 3.6368 | 37791.2 | 123.7 % |
| Kernel 7 | Unroll inner loop | 3.3314 | 41255.6 | 135.1 % |
| Kernel 8 | GMEM loads | 2.8032 | 49047.3 | 160.6% |
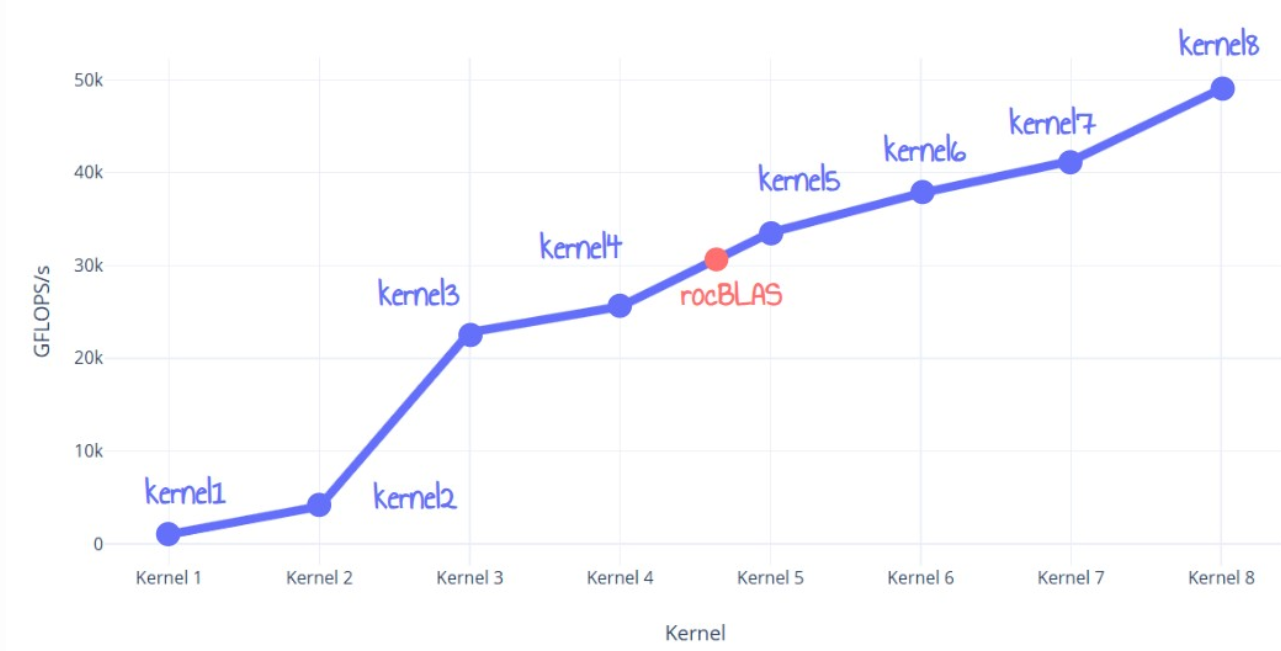
Conclusion
정말 흥미진진한 여정이었습니다. Windows에서 HIP를 시험해 보기 위한 간단한 실험으로 시작했지만, RDNA3의 하드웨어 세부 사항을 심층적으로 파헤치는 과정으로 이어졌습니다. 이 블로그를 시작하게 된 가장 큰 영감은 Simon Boehm이 CUDA에서의 행렬 곱셈에 대해 작성한 기술 게시물이였습니다. 훌륭하게 작성된 이 글은 Kernel 3에 분명히 영향을 미쳤습니다.
Windows에서 HIP 도구는 상당히 제한적입니다. 예를 들어, RGP는 기본적으로 뱅크 충돌을 표시하지 않습니다. 하지만 충분한 연습을 통해 명령어 타이밍 뷰를 사용하여 대부분의 성능 병목 현상을 분석할 수 있게 됩니다.
성능 결과는 rocBLAS보다 60% 더 뛰어나지만, 현재 상태에서는 이 코드가 확장성이 부족합니다. 더욱이, 사용자 지정 ISA 최적화를 수행하면 이러한 변경 사항이 RDNA3에만 적용되어 이식성이 제한됩니다. 코드베이스가 커질수록 수정 사항을 구현하기가 점점 더 어려워집니다.
다만, 이 개인 프로젝트의 목표는 유지 관리 용이성이나 유연성에 대한 걱정 없이 성능을 한계까지 끌어올리는 것이었습니다. 행렬 곱셈은 단 몇 줄의 코드로 구현할 수 있지만, 최적화된 구현을 작성하는 것은 엄청나게 어려운 일입니다. 저희는 순진한 커널과 최고 커널 간의 50배 속도 향상을 달성했는데, 제 경험상 HIP C++만으로는 불가능했을 것입니다. 이는 OpenAI의 Triton과 같은 프로젝트의 가치를 보여주는데, 특히 흥미롭고 앞으로 탐구해 볼 가치가 있다고 생각합니다.
거의 50 TFLOP/s에 도달한 것은 확실한 성과이지만, 아직 완전히 VALU에 도달하지는 못했습니다. 이는 앞으로 더 많은 성능 향상이 가능할 것으로 예상됩니다. 아직 테스트하지 않은 기술 중 하나는 LDS 이중 버퍼링인데, 이는 이러한 장벽 중 하나를 제거하고 SIMD 전체에서 LDS 명령어의 분산을 개선할 수 있는 잠재력을 가지고 있습니다.
마지막으로, 커널 4에 사용된 접근 방식에 영감을 준 LDS 최적화 브레인스토밍 세션을 진행해 주신 Francois Guthmann에게 감사드립니다. 이 프로젝트는 재미있고 통찰력 있는 시간이었습니다. 앞으로 더 많은 최적화를 연구할 수 있기를 기대합니다.
8개 커널의 모든 코드는 여기 github에서 확인하실 수 있습니다.
- HIP(Heterogeneous-Compute Interface for Portability)은 AMD가 개발한 C++ 기반의 병렬 컴퓨팅 API 및 런타임 라이브러리로, CUDA와 유사한 프로그래밍 모델을 제공하면서도 이식성을 고려한 설계가 특징을 가진다. AMD의 ROCm(Radeon Open Compute) 플랫폼에서 GPU 가속을 활용할 수 있도록 개발되었다.
- Cuda와 매우 유사한 코드구조를 가지며, 코드 변환을 쉽게 할 수 있도록 설계되었다. hipify를 사용하면 기존 CUDA코드를 HIP코드로 자동 변환할 수 있음
- AMD 및 Nvidia GPU도 동일 코드로 지원한다.
- CUDA와 OpenCL의 장점 결합
단점으로는 윈도우 지원이 제한적이며, Nvidia GPU에서는 CUDA보다 성능이 떨어질 수 있다. [본문으로]
- rocBLAS는 AMD의 ROCm 플랫폼을 위한 고성능 선형 대수 연산 라이브러리로, BLAS(Basic Linear Algebra Subprograms) 기능을 제공한다. HIP(Heterogeneous-Compute Interface for Portability) 프로그래밍 언어로 구현되어 AMD GPU에 최적화되어 있다. https://rocm.docs.amd.com/projects/rocBLAS/en/latest/how-to/what-is-rocblas.html?utm_source=chatgpt.com [본문으로]
- 행렬 계산(또는 일반적인 병렬 연산)에서 컴퓨팅 성능이 연산 속도에 의해 제한되는 상태를 의미. 즉, 연산을 수행하는 데 필요한 CPU 또는 GPU의 연산 성능(FLOPS)이 병목이 되는 경우 [본문으로]
- 이 링크를 작성했을 당시 Windows 11에서 사용 가능한 최신 버전인 ROCm 6.2.4를 사용했습니다. [본문으로]
- Radeon Graphic Profiler는 Windows에서 권장되는 프로파일러입니다. [본문으로]
- 저는 rocBLAS의 작동 방식을 분석하는 데 많은 시간을 들이지 않았지만 ROCBlas repo를 탐색해 본 결과 rocBLAS는 Tensile이라는 프로젝트를 사용하여 AMD GPU에 대한 고도로 최적화된 GEMM 코드를 생성하는 것으로 보입니다. [본문으로]
- VALU (Vector ALU, Vector Arithmetic Logic Unit)은 GPU에서 벡터 연산을 수행하는 연산 유닛(Execution Unit)으로, 이는 GPU 아키텍처에서 SIMD(Single Instruction, Multiple Data) 방식으로 병렬 연산을 수행하는 핵심 구성 요소이다. [본문으로]
- ROCm performance guidelines [본문으로]
- 루프 언롤링(Loop Unrolling)은루프(loop)의 반복 횟수를 줄이기 위해, 루프 내부 연산을 반복적으로 복제하는 최적화 기법을 말한다.
- Unrolled가 표시된 경우:
> 루프가 언롤링되어 개별 명령어로 변환됨 (루프가 펼쳐진 상태).
> 이는 성능 최적화를 위한 일반적인 기법으로, 레지스터 압박이 크지 않다면 GPU에서 성능이 향상될 수 있음.
- 루프가 Unrolled되지 않은 경우 (루프가 그대로 남아있는 경우):
> 루프가 유지된 상태로 실행됨.
> 루프 카운터(인덱스 증가, 조건 검사)가 남아 있어 약간의 성능 오버헤드가 발생할 수 있음.
> 하지만 너무 많은 언롤링은 레지스터 사용량 증가로 인해 성능 저하를 초래할 수도 있음. [본문으로] - Wavefront(웨이브프런트)는 AMD의 GPU에서 사용되는 개념으로, 여러 개의 병렬 스레드가 하나의 단위로 실행되는 그룹을 의미한다. NVIDIA에서는 같은 개념을 Warp(워프)라고 부른다 [본문으로]
- 냅킨 수학(napkin math)은 종종 코드를 작성하지 않고 가정과 참조 번호를 사용하여 결과를 빠르게 추정하는 방법입니다. "봉투 뒷면 계산-Back of the envelope"과 비슷합니다. 활용되는 예는 아래와 같습니다.
- 데이터 저장소의 처리량 추정
- MySQL 트랜잭션과 초당 fsync가 항상 동일한지 추정
- 데이터베이스 페이지를 방문하는 쿼리의 응답 시간 추정
- 기준점을 달러로 변환 [본문으로] - AMD GPU 아키텍처에서 자주쓰이는 개념으로 워크그룹(Workgroup) 내의 쓰레드들이 공유할 수 있는 메모리 공간으로,
전역 메모리(Global memory)보다 훨씬 빠른 접근 속도를 가집니다. Nvidia의 Shared Memory와 유사한 개념 [본문으로] - 내부 루프를 unroll 하면서 더 많은 LDS접근이 발생하고 컴파일러가 이를 최적화 하기위해 더 많은 데이터를 미리 로드함에 따라 커널 코드가 커지고 복잡해지며 결과적으로 성능향상이 없거나 오히려 저하되는 상황 [본문으로]
'Technical Report > Graphics Tech Reports' 카테고리의 다른 글
| Bent Normal 이란? (0) | 2025.04.27 |
|---|---|
| hlsl : 고급쉐이더 언어(High Level Shader language)란? (0) | 2025.04.27 |
| PLS(Pixel Logical Storage)와 FBF(Frame Buffer Fetch)의 차이 (0) | 2024.10.18 |
| DX11, DX12 렌더링 기본 구조 비교(작성중) (0) | 2024.10.17 |
| FBX Export Geometry options (6) | 2023.10.26 |
